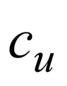. 1

Свойства регулярных отображений

1. Регулярное отображение непрерывно в обе стороны, т.е. достаточно близким точкам при отображении в одну сторону и в другую соответствуют сколь угодно близкие точки.

2. При регулярном отображении внутренние точки области D переходят во внутренние точки области G; граничные точки области D — в граничные точки области G и, наоборот, при обратном отображении.

3. При регулярном отображении кривая отображается в кривую.

4. Абсолютная величина якобиана при регулярном отображении равна пределу отношения меры отображенной области и первоначальной при стягивании их в точку:

d — диаметр области.

Таким образом, — коэффициент растяжения областей или величина искажения масштаба в точке z при отображении с помощью функции

Выведем формулу для нахождения коэффициента:

(по КРЭДу) или .

Тогда, коэффициент растяжения будет равен . (14)

Определение 36.Регулярное отображение области D плоскости (Oxy) на область G плоскости (Оuv) посредством гармонической пары или, что то же самое, аналитической функции, называется конформным, если в каждой точке оно обладает свойствами сохранения углов и постоянства растяжений.

Если представить себе плоскости (z) и совмещенными, то каждый малый вектор с вершиной в точке z0 при отображении будет перенесен вершиной в , растянут в k0 раз и повернут на угол α0. Поэтому и вся малая окрестность точки z0 при рассматриваемом отображении испытает поступательный перенос, всестороннее растяжение и поворот. Образ каждой малой фигуры, расположенной в области G, будет, с точностью до малых высшего порядка, геометрически подобен прообразу, т.е. малый круг переходит в круг, а углы между пересекающимися линиями сохраняются.

Лемма. При аналитическом отображении ориентация плоскости сохраняется, т.е. если обходить малый замкнутый контур плоскости (z) в некотором направлении, то и образ будет обходиться в том же направлении. И обратно, если некоторое отображение плоскости сохраняет подобие бесконечно малых фигур (или даже только углы между пересекающимися линиями) и ориентацию плоскости, то это отображение аналитическое.

В связи со сказанным можно дать другое определение конформности:

Определение 37.Взаимно однозначное отображение некоторой плоской области, при котором сохраняются подобие бесконечно малых фигур и ориентация плоскости, называется конформным; если подобие сохраняется, но ориентация меняется на противоположную, то отображение называется антиконформным.

Теорема 8.Отображение посредством аналитической функции конформно при условии, что якобиан .

Рассмотрим подробнее сказанное о сохранении углов и постоянстве растяжений при конформных отображениях.

Пусть — аналитическая функция в области D. Пусть задается взаимно-однозначное отображение области D плоскости (z) на область G плоскости посредством данной аналитической функции. Если точка (x,y) на плоскости (Oxy) описывает некоторую линию Г, расположенную в области D, то соответствующая точка (u,v) на плоскости (Оuv) опишет линию Г /, расположенную в области G (рис. 15).

Линию Г / называют отображением или образом линии Г на плоскость (Оuv) с помощью аналитической функции.

1) О сохранении углов.

Возьмем на линии Г точку (см. рис. 15). Этой точке на линии Г / соответствует точка Проведем к линии Г касательную L в точке (x0, y0), а к линии Г / — касательную в точке

Пусть α — угол, на который нужно повернуть касательную L, чтобы ее направление совпало с направлением прямой , т.е. это угол между касательными к первоначальной и отображенной кривым: .

Можно доказать, что .

Пусть — угол между осью (Ох) и касательной L к кривой Г, тогда /- угол между осью (Оu) и касательной к кривой Г/, угол между L и . Если поворот от L к происходит против часовой стрелки, если поворот от L к происходит по часовой стрелке.

Геометрический смысл аргумента производной:

— (15)

аргумент производной функции в точке геометрически равен углу , на который нужно повернуть касательную L в точке к кривой Г, чтобы получить касательную в точке ω0 к образу этой кривой Г/.

Рассмотрим другую линию γ, также проходящую через точку (x0, y0), и ее отображение — линию , проходящую через точку (рис. 15). Пусть l — касательная к кривой γ в точке (x0, y0), — касательная к кривой в точке

Для того чтобы направление прямой l совпало с направлением прямой надо и в этом случае прямую l повернуть на угол α, т.к. α зависит только от значения производной и не зависит от уравнения кривой.

Вывод 1. Две произвольные линии, пересекающиеся в точке (x0, y0), отображаются посредством функции в две соответствующие линии, пересекающиеся в точке так, что угол β между касательными к данным и между касательными к отображенным линиям один и тот же.

Замечание. Из свойства сохранения углов вытекает, в частности, что линии и плоскости (x,y) образуют два взаимно ортогональных семейства линий. Это дает возможность, задаваясь различными аналитическими функциями , получать разнообразные ортогональные системы координат на плоскости.

2) О постоянстве растяжений.

Рассмотрим коэффициент растяжения k. Пусть аналитическая функция отображает кривую Г1 в кривую γ1, кривую Г2 в кривую γ2, причем точка отображается в точку ω0, , (рис. 16).

Тогда — предел отношения растяжений или .

Замечание. При конформном отображении сохраняется подобие лишь бесконечно малых фигур, тогда как форма конечных фигур может существенно измениться. Например, квадрат плоскости (z), разбитый на 4 квадратика, может отобразиться на криволинейную фигуру с прямыми углами на плоскости (рис. 17). Дело в том, что хотя каждый малый участок плоскости (z) при отображении испытывает всестороннее растяжение и поворот, но для разных участков коэффициенты растяжения и углы поворота различны, что и приводит к такому искажению.

Пусть отрезок АВ посредством аналитической функции отображается в кривую (рис. 18). Тогда коэффициент растяжения — предел отношения длины дуги к длине отрезка. Следовательно, и любой другой отрезок растягивается ровно в k раз в плоскости (Оuv) при этом отображении.

При k > 1 имеет место растяжение, при k < 1 — сжатие.

Ранее вывели, что коэффициент растяжения может быть найден по формуле (14): .

Из теоремы 5 известно, что производная аналитической функции в точке z0 находится по формуле (11): Найдем модуль полученной после дифференцирования ФКП : и сравним полученное выражение с выражением (14). Видно, что . Для существования отображения должно быть , что гарантирует теорема 8, так как .

Геометрический смысл модуля производной:

— (16)

модуль производной функции в точке геометрически равен коэффициенту растяжения в точке при отображении .

Вывод 2. При отображении аналитической функцией наблюдается постоянство растяжений (сжатий), следовательно, отображение, осуществляемое аналитической функцией, конформно.

Определение 38.Функция называется однолистной в области D, если любым различным значениям , взятым из области D, соответствуют различные значения функции . Другими словами, если функция, обратная к , однозначная, то отображение называется однолистным.

Однолистность означает, что при отображении плоскость (z) покрывает плоскость только один раз.

Критерий конформности отображения:Для того чтобы отображение области D, задаваемое функцией , было конформным, необходимо и достаточно, чтобы была однолистной и аналитической в области D функцией, причем всюду в D.

Общий вывод из 1) и 2).Геометрический смысл модуля и аргумента производной аналитической функции состоит в том, что при отображении, осуществляемом этой функцией, удовлетворяющей условию , коэффициент растяжения k определяет коэффициент преобразования подобия бесконечно малого линейного элемента в точке z0 , а α — угол поворота этого элемента.

Пример 26.Найти коэффициент растяжения и угол поворота в точке для отображения

Комплексного переменного, геометрический смысл производной