7 ().
—
1.
F= 600 , .
:
1. ;
2. .
.
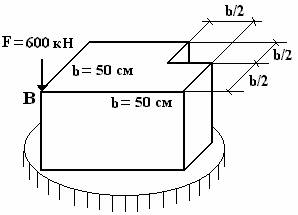
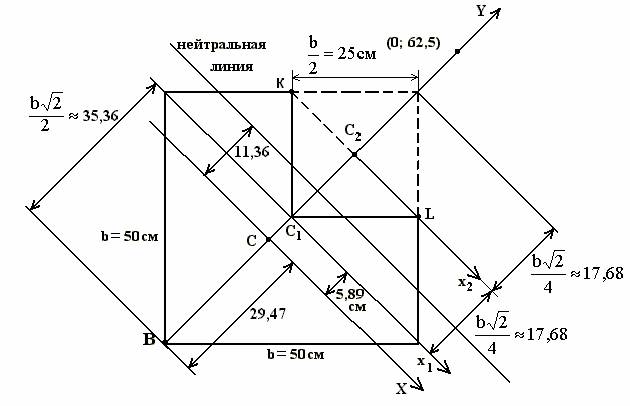
1. .
2. . , Y .
3. ( ). .
11Y ;
1 2 11Y.
,
1, 2 .
= 1 2 .
1 = b2 = 2500 2
( = 0; = -5,89) 11Y.
X Y .
, XY .
4. .
1 = 5,89 1;
2= 5,89 + 17,68 = 23,57 2.
5. ( ) .
6. .
,
N, N .
(N=0; N=11,36) .
7. ,
, , .
8. . , .
L yK = L = 23,57 .
: ,
2.
.
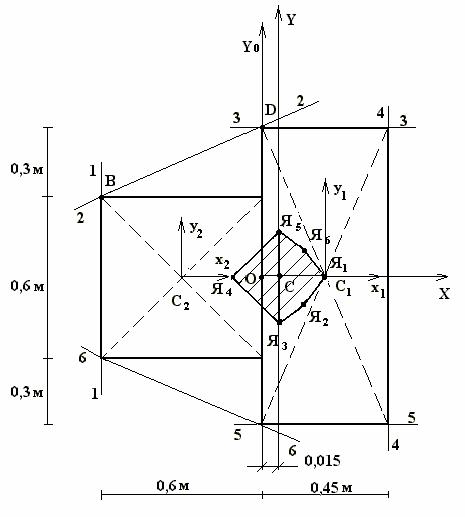
.
1. .
2. , ( ). 6 — 6 .
3. . , . Y0 ( Y0 ).
( ). 1 2 Y0.
— .
— .
— .
— .
.
( 12 ).
Y0 (0,015; 0). ( ).
Y Y0 .
, , .
X, Y .
4. .
Jx Jy.
— .
— .
( . 1 1, ,
;
, b 1, 1, . , , , , ).
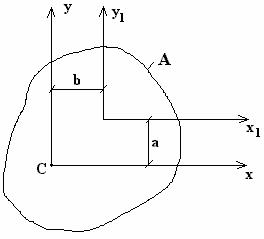
5. .
. .
1. 1 1.
. 11 Y, 1 X, F =0.
N 1 1 ( 1 1).
2. 2 2.
2 2 ( , )
(-0,615; 0,3) D(-0,015; 0,6)
D .
(1)
(2)
(1) (2)
(3)
(3) (2)
3. 3 3.
. 3 3 X, 3 Y, F =0.
N 3 3 ( 3 3).
4. 4 4.
. 4 4 Y, 4 X, F = 0.
5. 5 6 3 2.
3.
(. 1). . , . 2.
:
1) ,
2) .
.1 .2
.
(. ). :
.
.
, . ,
, ,
. 3.
.3
, . 1 1¢ (. . 3), . , .. 1. , 1:
1
( . Fp -2).
, 1¢, , 1, , , ..
. . , : 1, 2 3 (. . 3). ; , , . 1,
11, 1 . 3. 22 33, 2 3. , , , . , . 3, . . 3 . , .
4.
, (. 1). , . 2. .
:
1) , ;
2) .
.
, . . . 1 , , . Y, Z (.2) , .
.
.1 .2
, , .
, ; . , .
(. . 3).
.3
, .. , , 1 3 (. .3). 1 . , :
1 ,
, , 1 :
.
, 3, . 3
.
. , .
. , .. 1, 2, 3, 4, 5 (. . 3). 4, , . , , ( . 3). 4 . , , , , , ; . , 1, , ; 1 (),
, , 11 . 11, (. . 3). , , . ( ) . 3. , 44 55 , .. 4 5 . . 3 , .
5.
D =300 (. .). , ( ) .
:
1.
(.1) , , .
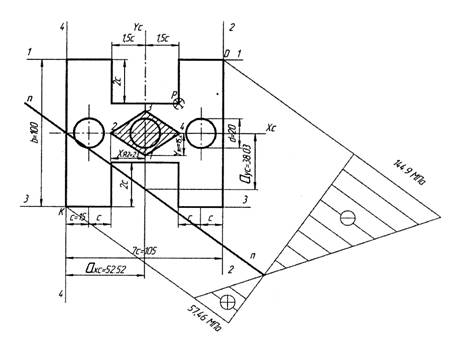
, .
:
2.
:
:
3.
, , :
=2,3 =2 ( .11). , , (). .1 n-n.
4.
D, D=5,25 D=5 , ,
, = ‑5,25 , = ‑5 .
(. .11).
5.
, , , I-I II-II (. .1).
, I-I , :
1 :
II-II =5,25 , =¥.
2:
, . III-III IV-IV, 3 4 :
= 0; = 15,2×10-3 ;
= 23,0×10-3 = 0.
1, 2, 3 4 (.1).
6.
, , . F= 200 = 20 A.
.
X Y , .
, , , . , . .
(. .):
= 90 = 0,09 ;
= 60 = 0,06 .
:
, ,
— X Y.
. :
4;
4.
:
2,
:
2;
2.
, X Y:
;
.
, , . (. .). , — B D .
:
;
(. .) :
= 0,12 ; = 0,03 .
= 5,39×104 /2 = 53,9 .
;
= 0,12 ; = 0,03 .
= 1,86×104 /2 = 18,6 .
7.
, , F, .
:
1) , F ; = 40 , b = 60 ;
2) F = 100 = 30 .
.
, , . X , , , . (1 2) . 1 2 .
1 (0,0); 2(0,04; 0), :
;
= 0.
, xy1 (0,0133; 0). Y, X. X Y .
.
, .
( ) : =(0,020,0133)+0,04 =0,0467 ; = 0,06 ;
:
, .
4,
4,
= 0,0133 ;
2.
2, 2;
, X Y :
X, Y (. .). , — . : (0,0467; 0,06); ( 0,0333; 0,12). , F.
, , .. :
, ,
(),
().
():
():
, , , .. = 103 .
8.
, , F, .
:
1) , F ;
2) F .
.
.
( ) :
:
, .
0, 0 n n (. .). , — . : (0,04; 0,06), (0,04; 0,06). , F:
, , ..
,
,
F
, .. = 567.
9.
, . , P, A. , P , . /2 /2.
.
P x y. :
,
P ( A).
x y
,
F , .
1. .
:
.
.
x, , x .
.
y : , y .
.
:
; .
2. .
, , :
; .
N N . . , , . 1, .
3. .
6 7, , . , , , 6 :
.
4. .
2 3, . , , , 2, :
.
5. :
/2; .
6. :
/2; .
7. . 6 7 :
.
10.
, .1, F=200 , . =40 , b=16 . Rt = 3 , R = 30 .
:
1. .
2. . .
3. ( ) Fmax .
4. .
.1
.
1. .
, Yo (. .1)
2. .
.
,
F
3.
, (. . 2).
4. . .
: (-60; 16) D(60; -32). dan, dan
.
.
.
.
. 2 .
5. Fmax.
, , st sc .
Fmax=425,8 , , .
.2
6. .
, , , , . , .
1-1: yo = 32 ,
.
2-2: , .
3-3: , .
4-4: ; ;
; ;
; ;
;
.
5-5: ; .
6-6: ; ;
; .
11.
P P(. .). .
.
:
, ,
.
A B:
A
B
, :
12.
, , Radm,t= 20 ; Radm,= 100 .
. , :
, ,
,
:
Fadm = 64 .
13.
, F, , . 1.
.
F :
,
. 2. 1, 2, 3 4 (. 3), y = ymax z = zmax,
, :
. 3.
:
.4. , .4.
14.
, . .
.
. . :
1 = 0,61,4/2 = 0,42 2; 2 = 0,51,4 = 0,7 2; 3 = 0,80,6 = 0,48 2; 4 = 0,32/2 = 0,1413 2.
= 1+2+3+4 = 1,74 2.
z z/ :
z:
:
;
z= 0, = b z =, = 0, :
()
, . , 1 2 , , bo = 1,016 ; = 0,7/0,6; = bo = 1,0160,7/0,6 = 1,185 .
()
1-2. , 1-2, 1 2 . , .
, 2 3 . = 0,7 ; bo= , ()
2-3 (. .).
, 3 4, 4 . bo , , bo , .. : = 0,74 , bo = 1,62 .
3-4.
5 z, ao =, bo = yC = 1,184 . () 5, ,
, 1 z. bo = 1,016 ; =. 1 :
1, 1-2, 2-3, 3-4 , 3-4 5 . , . , , .
15.
(a = 1,05 , b = 1 , = 0,15 , d = 0,2 ) D = 150 (.1).
:
1. ;
2. ( ) ;
3. .
.1
:
1. .
1.1. . (. 1) x y , . :
2.
1.2. . :
;
.
:
2;
2 .
1.3. . , , :
;
,
xP = 0,525 yP = 0,5 — ( D . 1). , , xC yC , , , .. , (). . 1 n-n.
2. ( ) . D, xD = 0,525 yD = 0,5 , , :
.
, xK = -0,525 yK = -0,5 :
.
(. 1).
3. . I-I II-II (. 1). , I-I , :
; = 0,5 .
I :
.
II-II = 0,525 , .
, 2:
.
, .. . , III-III, IV-IV 3 4 :
; .
1, 2, 3 4 , (. 1).
: KarimovI@rambler.ru
: , 450071, ., 21
Задача:
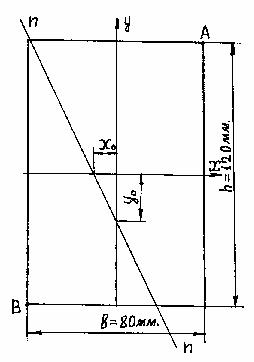
Бетонный столб заданного сечения сжимается силой F=100кН, приложенной в точке К. Требуется:
1) Найти положение нулевой линии и проверить прочность, если [σс]=15МПа, [σр]=0,5МПа.
2) Построить ядро сечения.

Для решения задачи необходимо знать геометрические характеристики сечения, то есть положение центра тяжести, величину площади, положение главных центральных осей и величины главных центральных моментов инерции. С этого и начнем. Так как сечение имеет одну ось симметрии у, то она является одной из главных центральных осей. Другая главная центральная ось пройдет перпендикулярно оси симметрии через центр тяжести сечения. Нам неизвестно его положение на оси симметрии. Для его определения выберем произвольную ось, перпендикулярную оси симметрии (например, х1), вычислим статический момент сечения относительно этой оси, а затем разделим его на площадь сечения. Это и будет расстояние от оси х1 до центра тяжести сечения С.
Но поскольку сечение представляет собой сложную фигуру, то предварительно «разобьем» его на простые части и покажем на чертеже собственные центральные оси каждой из этих частей (х1, у1; х2, у2; х3, у3; х4, у4). Итак:

Тогда
Откладываем эту ординату вверх от оси х1 по оси симметрии, это и есть центр тяжести сечения С, через который проводим вторую главную центральную ось х.
Остается вычислить осевые моменты инерции относительно каждой из осей.

Тогда квадраты радиусов инерции относительно главных центральных осей будут:
Для определения положения нулевой линии в сечении необходимо вычислить величины отрезков, которые нулевая линия отсекает от главных центральных осей инерции, по формулам:
Здесь: хF и уF — координаты точки приложения силы F в системе главных центральных осей. В нашем случае : хF =50см, уF=30-12,8=17,2см.
Тогда
Отложив эти отрезки с учетом их знаков, проводим нулевую линию (см. чертеж), которая делит сечение на две зоны: сжатую и растянутую:

Для оценки прочности надо найти наибольшие напряжения: сжимающие и растягивающие, а затем сопоставить их с допускаемыми напряжениями.
Наибольшее сжимающее напряжение возникает в той точке сжатой зоны, которая наиболее удалена от нулевой линии. Судя по чертежу, эта точка К с координатами хК=50см и уК=17,2см. Подставляя эти координаты в формулу напряжений, имеем:

Наиболее удаленной от нулевой линии точкой в растянутой зоне является точка В с координатами хВ=50см и уВ=- (30+12,8)=-42,8см. В ней и возникает наибольшее растягивающее напряжение:

Проверка прочности:
Следовательно, заданная прочность не обеспечена, так как в растянутой зоне условие прочности не выполняется.
Для построения ядра сечения задаемся несколькими конкретными положениями нулевой линии так, чтобы она только касалась контура самого сечения и нигде его не пересекала, и для каждого такого положения нулевой линии вычисляем координаты соответствующего ей центра давления. Эти точки и определят контур самого ядра сечения.
Подставляя, имеем:
На схеме показывает центр давления 1.
Для нулевой линии II отрезок, отсекаемый от оси х,составит величину
От оси у Н.Л. II отсекает отрезок
Тогда соответствующий центр давления расположится в точке с координатами:
На схеме это точка 2.
Нулевая линия III симметрична нулевой линии II, поэтому и правая точка 3 симметрична точке 2.
А нулевая линия IV симметрична линии I. Следовательно, ядровая точка 4 симметрична точке 1.
Наконец, проводим нулевую линию V по нижней кромке сечения. Она отсекает от главных центральных осей отрезки: ах=∞ и ау=-42,8см. Соответствующие координаты центра давления будут:
На схеме это точка 5.
Поскольку переходы нулевых линий из одного положения в смежное с ним происходили путем поворота вокруг неподвижных точек, то и перемещение центра давления от одной ядровой точки к другой происходит по прямой линии, соединяющей эти точки. На этом основании соединяем найденные ядровые точки прямыми, которые и ограничивают область, называемую ядром сечения.

Решение типовых задач по сопромату.
Пример решения задачи на растяжение и сжатие
.
Условие задачи на растяжение и сжатие
Стальной стержень (модуль Юнга кН/см2) с размерами см; см, см и площадью поперечного сечения нижнего участка см2, а верхнего — см2 нагружен внешними осевыми силами кН и кН. Построить эпюры продольных сил и нормальных напряжений . Оценить прочность стержня, если предельное напряжение (предел текучести) кН/см2, а допускаемый коэффициент запаса . Найти удлинение стержня .
Расчетная схема для задачи на растяжение и сжатие
рис 3.2
Решение пример задачи на растяжение и сжатие
Определяем значение опорной реакции , возникающей в заделке
Учитывая, что , направим опорную реакцию вниз. Тогда из уравнения равновесия находим:
кН.
Строим эпюру продольных сил
Разбиваем длину стержня на три участка. Границами участков являются сечения, в которых приложены внешние силы и (или) изменяется размер поперечного сечения стержня.
Воспользуемся методом сечений. Делаем по одному сечению в произвольном месте каждого из трех участков стержня.
Cечение 1 — 1. Отбросим (или закроем листком бумаги) верхнюю часть стержня (рис. 3.2, б). Само сечение 1 — 1 мысленно считаем неподвижным. Мы видим, что внешняя сила растягивает рассматриваемую нижнюю часть стержня. Отброшенная нами верхняя часть стержня противодействует этому растяжению. Это противодействие мы заменим внутренней продольной силой , направленной от сечения и соответствующей растяжению. Разрушения стержня не произойдет только в том случае, если возникающая в сечении 1 — 1 внутренняя продольная сила уравновесит внешнюю силу . Поэтому очевидно, что
кН.
Сечение 2 — 2. Внешняя сила растягивает рассматриваемую нами нижнюю часть стержня, а сила ее сжимает (напомним, что 2 — 2 мы мысленно считаем неподвижным). Причем, согласно условию задачи, . Чтобы уравновесить эти две силы, в сечении 2 — 2 должна возникнуть внутренняя сила , противодействующая сжатию, то есть направленная к сечению. Она равна:
кН.
Сечение 3 — 3. Отбросим теперь часть стержня, расположенную ниже этого сечения. Внутренняя продольная сила должна уравновесить внешнюю (реактивную) сжимающую силу . Поэтому она направлена к сечению и равна:
кН.
Легко убедиться в том, что полученный результат не изменится, если мы отбросим не нижнюю, а верхнюю часть стержня. В этом случае продольная сила также противодействует сжатию. Она равна:
кН.
При построении эпюры продольных сил будем пользоваться следующим правилом знаков: внутренняя продольная сила, возникающая в поперечном сечении стержня, считается положительной, если она противодействует растяжению стержня, и отрицательной, если она противодействует его сжатию. Оно вводится для того, чтобы можно было наглядно видеть, какая часть стержня испытывает деформацию растяжения, а какая часть — деформацию сжатия. Это обстоятельство может оказаться крайне важным, в частности для стержней из хрупкого материала, которые имеют разные допускаемые напряжения на растяжение и на сжатие.
Таким образом, мы установили, что в любом сечении нижнего участка стержня внутренняя продольная сила противодействует растяжению и равна кН. В любом сечении среднего и верхнего участков стержня имеет место деформация сжатия, поэтому кН.
Для построения эпюры продольных сил проводим тонкой линией ось, параллельную оси стержня z (рис. 3.2, д). Вычисленные значения продольных сил в выбранном масштабе и с учетом их знака откладываем от этой вертикальной оси. В пределах каждого из участков стержня продольная сила остается постоянной, поэтому мы как бы «заштриховываем» горизонтальными линиями соответствующий участок.
Отметим, что каждая линия «штриховки» (то есть ордината эпюры) в принятом масштабе дает значение продольной силы в соответствующем поперечном сечении стержня.
Полученную эпюру обводим жирной линией.
Анализируя полученную эпюру, мы видим, что в местах приложения внешних сил на эпюре имеет место скачкообразное изменение продольной силы на величину, равную значению соответствующей внешней силы. Причем изменение поперечного размера стержня, как это видно из рис. 3.2, д, никак не сказывается на характере эпюры .
Строим эпюру нормальных напряжений
Нормальное напряжение, возникающее в k-м поперечном сечении стержня при растяжении (сжатии), вычисляется по следующей формуле
,
где и — продольная сила и площадь k-го поперечного сечения стержня соответственно.
В первом поперечном сечении стержня нормальное напряжение равно
кН/см2,
во втором —
кН/см2,
в третьем —
кН/см2.
Строим по вычисленным значениям эпюру (рис. 3.2, е). В пределах каждого из участков стержня напряжения постоянны, то есть эпюра напряжений параллельна оси. Заметим, что в отличие от эпюры N, на эпюре «скачок» имеет место не только в местах приложения внешних сил, но и там, где происходит изменение размеров поперечного сечения стержня.
Оцениваем прочность стержня
Сопоставляем наибольшее (по модулю) нормальное напряжение , которое в нашем примере возникает во втором сечении стержня, с допускаемым напряжением . Напомним, что допускаемое напряжение представляет собой долю от предельного напряжения , то есть от напряжения, при котором начинается разрушение материала. Разрушение стали, как пластичного материала, начинается при появлении значительных остаточных деформаций. Поэтому для стали предельное напряжение равно пределу текучести: . Тогда
кН/см2.
Условие прочности имеет вид . В нашем случае
кН/см2 > кН/см2,
следовательно, прочность стержня на втором участке не обеспечена.
Таким образом, площадь поперечного сечения стержня на втором участке, равную см2, нам необходимо увеличить.
Несложный анализ показывает, что на других участках стержня условие прочности выполняется.
Из условия прочности определяем требуемую площадь поперечного сечения стержня на втором участке:
см2.
Принимаем на втором участке см2.
Вычисляем удлинение всего стержня
При переменных по длине стержня значениях продольной силы и площади поперечного сечения удлинение вычисляется по формуле
,
где E — модуль Юнга, а — длина соответствующего участка стержня.
Тогда
см.
Таким образом, длина стержня уменьшается на мм.
Задача по сопромату на растяжение и сжатие для самостоятельного решения
Условие задачи на растяжение и сжатие
Стальной стержень (модуль Юнга кН/см2) находится под действием внешних осевых сил и (рис. 3.1). Построить эпюры продольных сил и нормальных напряжений . Оценить прочность стержня, если предельное напряжение (предел текучести) кН/см2, а допускаемый коэффициент запаса . Найти удлинение стержня .
Схемы для задачи на растяжение и сжатие
Исходные данные к задаче на растяжение и сжатие
Номер схемы | F, см2 | a, м | b, м | c, м | P, кН |
1 | 2,0 | 1,2 | 1,4 | 1,6 | 11 |
2 | 2,2 | 1,4 | 1,6 | 1,4 | 12 |
3 | 2,4 | 1,8 | 1,6 | 1,2 | 13 |
4 | 2,6 | 1,6 | 2,0 | 1,0 | 14 |
5 | 2,8 | 2,0 | 1,8 | 1,2 | 15 |
6 | 3,0 | 2,2 | 1,6 | 1,4 | 16 |
7 | 3,2 | 2,4 | 1,4 | 1,6 | 17 |
8 | 3,4 | 2,6 | 1,2 | 1,8 | 18 |
9 | 3,6 | 2,8 | 1,0 | 1,4 | 19 |
3,8 | 2,4 | 1,6 | 1,2 | 20 |
- Ковнер, «Очерки истории M.».
- А.В. Ланцова, Е.В. Санарова, Н.А. Оборотова и др. Разработка технологии получения инъекционной лекарственной формы на основе отечественной субстанции производной индолокарбазола ЛХС-1208 // Российский биотерапевтический журнал. 2014. Т. 13. № 3. С. 25-32.
- Pund A. U., Shandge R. S., Pote A. K. Current approaches on gastroretentive drug delivery systems. Journal of Drug Delivery and Therapeutics. 2020; 10(1): 139–146. DOI: 10.22270/jddt.v10i1.3803.
- https://www.soprotmat.ru/sloz2.htm.
- https://prosopromat.ru/zadachi/zadachi-na-slozhnoe-soprotivlenie/vnecentrennoe-rastyazhenie-szhatie.html.
- https://sopromato.ru/tasks/rastyazhenie-i-szhatie.
- З.С. Смирнова, Л.М. Борисова, М.П. Киселева и др. Доклиническое изучение противоопухолевой активности производного индолокарбазола ЛХС-1208 // Российский биотерапевтический журнал. 2014. № 1. С. 129.
- Baas, «Geschichte d. Medicin».
- З.С. Смирнова, Л.М. Борисова, М.П. Киселева и др. Противоопухолевая эффективность прототипа лекарственной формы соединения ЛХС-1208 для внутривенного введения // Российский биотерапевтический журнал. 2012. № 2. С. 49.