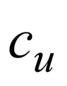Сила упругости

Содержание

Научный журнал
Современные наукоемкие технологии
ISSN 1812-7320
«Перечень» ВАК
ИФ РИНЦ = 1,021

Авторы
Резюме
Файлы

Иванов Е.М.

Показано, что работа растяжения пружины A>kxm2 , где k — жесткость пружины, xm — максимальное растяжение. При вычислении работы надо использовать значения x и dx, полученные из решения уравнения движения.

It is shown, that work of a stretching of a spring A>kxm2 , where k — rigidity of a spring, xm — the maximal stretching. At calculation of work it is necessary to use values x and dx, the equations of movement received from the decision.

Рассмотрим спиральную пружину, один конец которой закреплен (рис. 1а), а к другому прикреплен груз массой m. Если пружину растянуть или сжать, то возникает сила F, стремящаяся вернуть тело в положение равновесия. При небольших растяжениях x справедлив закон Гука — сила пропорциональна растяжению пружины: F = -kx. Постоянная k называется коэффициентом упругости, или жесткостью пружины. Знак минус означает, что сила F направлена в сторону, противоположную смещению x, т.е. к положению равновесия x = 0. Геометрически (рис. 1b) , k = tgβ, xm — максимальное (амплитудное) растяжение пружины.

В курсах физики утверждается, что работа при растяжении от x = 0 до xm будет равна

(1)

и эта работа равна потенциальной энергии пружины, растянутой (или сжатой) на величину xm и обладающей жесткостью k. Однако это одно из заблуждений классической механики. Растягивающей силой, равной F = kx, нельзя растянуть пружину даже на долю микрона. Чтобы растянуть пружину, надо приложить растягивающую силу в виде (F1 + k1x ), где F1 >0 (рис. 2а). Уравнение движения (II закон Ньютона) запишем в следующем виде:

(2)

Решение при нулевых начальных условиях (при t = 0, x =0 и V =0) имеет вид

Из решения следует, что если F1 =0, то растяжения пружины не происходит. Амплитудные значения (при x = xm):

Работу вычисляем по формуле , где F = F1 — (k — k1)x, а x и dx определяются из выражений (3) и (4). Работа, совершаемая растягивающей силой

(5)

Работа, совершаемая силой упругости пружины

(6)

Из соотношения (5) следует, что работа, совершаемая растягивающей силой, не зависит от величин F1 и k1 и равна работе

(5а)

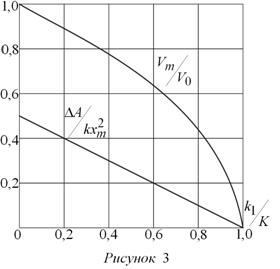
совершаемой постоянной силой F0, при этом работа, совершаемая силой упругости пружины A-0 = -kxm2 разность работ ΔA0 = kxm2 / 2 , конечная скорость при x = xm На рис. 3 даны графики зависимостей Vm / V0 и ΔA = kxm2 от величины отношения K1 / K. ΔA — кинетическая энергия груза.

Рассмотрим случай растягивающей силы FP > F0 (рис.2b) FP = F2 + k2x = F2 — b2x , где b2 = -k2 = tgα. Дифференциальное уравнение движения имеет вид:

(7)

Его решение при нулевых начальных условиях имеет вид:

; (8)

(9)

Амплитудные значения (при x = xm): xm = F2 / mω2; ; .

Работа, совершаемая растягивающей силой

(10)

Работа, совершаемая силой упругости пружины

(11)

Кинетическая энергия груза при x = xm

(12)

На рис. 4 даны графики изменения безразмерных комплексов ΔA / kxm2 и Vm / V0 в зависимости от величины отношения k2 / k.

Рассмотрим третий способ растяжения пружины с грузом (рис. 2с). Прикладываем растягивающую силу Fa >>F0 для растяжения пружины на некоторое расстояние xa, затем сила Fa отключается, а оставшийся отрезок пути, равный xm — xa, груз проходит по инерции, используя запас кинетической энергии Ka, приобретенный в точке xa. Для первого участка пути дифференциальное уравнение имеет вид

(13)

Его решение при нулевых начальных условиях:

; (14)

(15)

Время движения до x = xa

(16)

Работу вычисляем по формуле , где F(x) = Fa — kx, а x и dx определяются выражениями (14) и (15). Работа растяжения на участке до x = x0

(17)

Работа, совершаемая силой упругости пружины на этом же участке

(18)

Кинетическая энергия, приобретенная грузом:

(19)

Для второго участка уравнение движения имеет вид

(20)

Начальные условия для этого уравнения примем в виде: при t = 0 координата x = xa, скорость Va определяется выражением (15) при t = ta. Решение будет иметь вид:

(21)

(21a)

Работа силы упругости пружины на участке от x = xa до xm определится интегралом , где x и dx определяются выражениями (21) и (21а):

(22)

где tm ─ время движения груза от x=xa до x = xm. Условием достижения этой точки является равенство начальной кинетической энергии Ka работе силы упругости пружины A2. Это равенство сводится к трансцендентному уравнению

(23)

где a = kxa2 / 2; b = Ka — a; c = kxaVa / 2ω; φ = ωtm.

Приведем численный пример. Груз массой m = 1 кг, прикрепленный к пружине с жесткостью k = 400 Н/м, растягивается силой F0 = 80 Н на расстояние xm = 0,2. Работа силы растяжения Дж, работа силы упругости пружины Дж, время t = 0,0785 с.

Проведем растяжение силой Fa по схеме, показанной на рис. 2с. Расчет сведем в таблицу 1.

Таблица 1.

Fa [H]	Ka [Дж]	ta [c]	xa [м]	A+ [Дж]	A- [Дж]	tm [c]
8000	8	0,0005	0,001	16	-8	0,078
800	7	0,00468	0,00876	14,015	-7,015	0,0762
200	6	0,0176	0,0309	12,19	-6,19	0,0696
80	3,75	0,0377	0,054	8,088	-4,338	0,0597

Таким образом, только в случае растяжения пружины с грузом по схеме, показанной на рис.2с, можно затратить работу на растяжение A+, близкую к потенциальной энергии растянутой пружины П = kxm2 / 2.

Библиографическая ссылка

Иванов Е.М. РАБОТА ДЕФОРМАЦИИ ПРУЖИННОГО МАЯТНИКА // Современные наукоемкие технологии. — 2007. — № 3. — С. 15-19;

URL: https://top-technologies.ru/ru/article/view?id=24676 (дата обращения: 26.06.2021).

Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»

(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация — это изменение формы тела, под действием приложенных сил.

Виды деформации

Деформация — это изменение формы, или размеров тела.

Есть несколько видов деформации:

сдвиг;
кручение;
изгиб;
сжатие/растяжение;

Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.

Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.

Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б — эта же линейка, деформируемая кручением.

Рис. 1. пластиковая линейка, деформированная изгибом — а) и кручением — б)

В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.

Растяжение пружины

Рассмотрим подробнее деформацию растяжения на примере пружины.

Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина (L_{0}) пружины.

Рис. 2. Сравнивая длину свободной пружины с длиной нагруженной, можно найти ее удлинение

Подвесим теперь к пружине груз. Пружина будет иметь длину (L), указанную на рисунке справа.

Сравним длину нагруженной пружины с длиной свободно висящей пружины.

[ large L_{0} + Delta L = L ]

Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину (L_{0}).

[ large boxed{ Delta L = L — L_{0} }]

( L_{0} left(text{м} right) ) — начальная длина пружины;

( L left(text{м} right) ) — конечная длина растянутой пружины;

( Delta L left(text{м} right) ) — кусочек длины, на который растянули пружину;

Величину ( Delta L ) называют удлинением пружины.

Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.

Примечание: Отношение — это дробь. Относительное — значит, дробное.

[ large boxed{ frac{Delta L }{ L_{0}} = frac{ L — L_{0}}{L_{0} } = varepsilon } ]

( varepsilon ) — это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.

Расчет силы упругости

Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.

Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.

Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.

Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо

Закон Гука

Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.

[ large boxed{ F_{text{упр}} = k cdot Delta L }]

Эту формулу назвали законом упругости Гука.

( F_{text{упр}} left( H right) ) — сила упругости;

( Delta L left(text{м} right) ) — удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) ) — коэффициент жесткости (упругости).

Какие деформации называют малыми

Закон Гука применяют для малых удлинений (деформаций).

Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.

Если же тело к первоначальной форме не вернется — малыми деформации назвать не получится.

Как рассчитать коэффициент жесткости

Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему — по оси.

Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости

Так как силы взаимно компенсируются, в правой части уравнения находится ноль.

[ large F_{text{упр}} — m cdot g = 0 ]

Подставим в это уравнение выражение для силы упругости

[ large k cdot Delta L — m cdot g = 0 ]

Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:

[ large boxed{ k = frac{ m cdot g }{Delta L} }]

(g) — ускорение свободного падения, оно связано с силой тяжести.

Соединяем две одинаковые пружины

В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.

Параллельное соединение пружин

На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.

Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины

Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).

Одна пружина:

[ large k_{1} cdot Delta L = m cdot g ]

Две параллельные пружины:

[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]

Так как правые части уравнений совпадают, левые части тоже будут равны:

[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]

Умножим обе части полученного уравнения на число 2:

[ large boxed{ k_{text{параллел}} = 2k_{1} } ]

Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной

Последовательное соединение пружин

Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.

Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.

На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).

Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений

Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины

Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).

Одна пружина:

[ large k_{1} cdot Delta L = m cdot g ]

Две последовательные пружины:

[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]

Так как правые части уравнений совпадают, левые части тоже будут равны:

[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

[ large k_{text{послед}} cdot 2 = k_{1} ]

Разделим обе части полученного уравнения на число 2:

[ large boxed{ k_{text{послед}} = frac{k_{1}}{2} } ]

Коэффициент жесткости (k_{text{послед}}) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной

Потенциальная энергия сжатой или растянутой пружины

Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.

Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией

Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).

Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:

[ large boxed{ E_{p} = frac{k}{2} cdot left( Delta L right)^{2} }]

( E_{p} left( text{Дж} right)) — потенциальная энергия сжатой или растянутой пружины;

( Delta L left(text{м} right) ) — удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) ) — коэффициент жесткости (упругости) пружины.

Выводы

Упругие тела — такие, которые сопротивляются деформации;
Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
Деформация — изменение формы, или размеров тела;
Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
Удлинение пружины — это разность ее конечной и начальной длин;
Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
Если пружины соединяют параллельно — коэффициент жесткости системы увеличивается;
А если соединить пружины последовательно — коэффициент жесткости системы уменьшится.

Решение. По закону Гука сила F, растягивающая пружину, пропорциональна растяжению пружины, т е. F=kx

Решение. По закону Гука сила F, растягивающая пружину, пропорциональна растяжению — страница №1/1

2.Работа переменной силы.

Вычисление работы, затраченной на растяжение или сжатие пружины.

Пример1: Какую работу совершает сила в 10Н при растяжении пружины на 2см?

Решение. По закону Гука сила F , растягивающая пружину, пропорциональна растяжению пружины , т.е. F=kx.

Используя условие , находим , т.е. F=500x.

Согласно формуле, получим

Упражнение:

Какую работу совершает сила в 8Н при растяжении пружины на 6см?

Какую работу совершает сила в 20Н при растяжении пружины на 4см?

Пример 2.Сила в 60Н растягивает пружину на 2см. Первоначальная длина пружины равна 14см. Какую работу нужно совершить, чтобы растянуть ее до 20см?

Решение:

Имеем и, следовательно , F=3000x. Так как пружину требуется растянуть на 0.06м, то

Упражнения:

3.Сила в 40Н растягивает пружину на 0.04м. Какую работу надо совершить, чтобы растянуть пружину на 0.02м?

Для сжатия пружины на 3см необходимо совершить работу в 16Дж. На какую длину можно сжать пружину, совершив работу в 144Дж?

5. Пружина в спокойном состоянии имеет длину 20см. Сила в 9.8Н растягивает ее на 2см. Определить работу, затраченную на растяжение пружины от 25см до 35см.

3. Давление жидкости.

Величина силы Р давления жидкости в ньютонах на

горизонтальную площадку вычисляется по формуле

где — плотность жидкости в , s —

площадь площадки в , h — глубина погружения площадки в м. Рассмотрим задачу определения давления жидкости на

вертикальную площадку.

Пример1: Треугольная пластинка с основанием 0.3 м и высотой 0.6 м погружена вертикально в воду так, что е вершина лежит на поверхности воды, а основание параллельно ей. Вычислить силу давления воды на пластинку.

Решение:

Разобьем пластинку на n тонких полосок. На глубине x выделим одну из них и обозначим через ее ширину. Приняв полоску за прямоугольник, найдем ее площадь :

Из подобия треугольников АВС и КВМ имеем::

откуда КМ=1/2х. Следовательно,

Суммируя элементарные давления на каждую из полосок и неограниченно увеличивая число делений n, найдем значение силы Р давления жидкости на всю пластинку:

Таким образом.

Пример2: Определить силу давления воды на стенку шлюза, длина которого 20м, а высота 5м. (считая шлюз доверху заполненным водой)

Решение:

Упражнения:

1. Вычислить силу давления воды на вертикальную прямоугольную пластинку, основание которой 30м, а высота 10м, причем верхний конец пластинки совпадает с уровнем воды.

2. Вычислить силу давления воды на вертикальную прямоугольную пластинку, основание которой 16м, а высота 24м, причем верхний конец пластинки находится на 10см ниже свободной поверхности воды.

3. Треугольная пластинка с основанием 0.9м и высотой 0.12 м погружена вертикально в воду так, что е вершина лежит на 0.03м ниже поверхности воды, а основание параллельно ей. Вычислить силу давления воды на пластинку.

4. Вычисление работы против сил межмолекулярного притяжения.

— внутреннее давление, обусловленное силами взаимодействия молекул.

Пример1: Некоторый газ количеством вещества 1 кмоль занимает объем . При расширении газа до объема была совершена работа А против сил межмолекулярного притяжения, равная 45,3 кДж. Определить поправку а, входящую в уравнение Ван-дер-Ваальса.

Дано: Определить: а

Решение.

Упражнение: 1. Кислород, массой 100г расширяется от объема 5л до объема 10л. Определить работу межмолекулярных сил притяжения при этом растяжении. Поправку а взять из примера 1.

2. Некоторый газ количеством вещества 0,25 кмоль занимает объем . При расширении газа до объема была совершена работа А против сил межмолекулярного притяжения, равная 1,42 кДж. Определить поправку а, входящую в уравнение Ван-дер-Ваальса.

5. Сила и плотность электрического тока.

где S — площадь поперечного сечения проводника.

Пример: Сила тока в проводнике сопротивлением R=50Ом равномерно растет от за время Определить выделившееся за это время количество теплоты.

Дано:

Определить: Q

Решение: Согласно закону Джоуля — Ленца для бесконечно малого промежутка времени,

По условию задачи сила тока равномерно растет, т.е. I=kt, где к — коэффициент пропорциональности

Тогда (1)

Проинтегрировав (1) и подставив выражение для k, найдем искомое количество теплоты:

Вычисляя получим Q=900 Дж.

Упражнение: 1. Сила тока в проводнике сопротивлением R=120Ом равномерно растет от за время Определить выделившееся за это время количество теплоты.

2. Сила тока в проводнике сопротивлением R=100Ом равномерно убывает от за время Определить выделившееся за это время количество теплоты.

Литература:

Haeser, «Handbuch der Gesch. d. Medicin».
М.П. Киселева, З.С. Шпрах, Л.М. Борисова и др. Доклиническое изучение противоопухолевой активности производного N-гликозида индолокарбазола ЛХС-1208. Сообщение II // Российский биотерапевтический журнал. 2015. № 3. С. 41-47.
Renouard, «Histoire de la medicine» (П., 1948).
https://top-technologies.ru/ru/article/view?id=24676.
https://formulki.ru/mehanika/sila-uprugosti.
https://davaiknam.ru/text/reshenie-po-zakonu-guka-sila-f-rastyagivayushaya-prujinu-propo.
Moustafine R. I., Bukhovets A. V., Sitenkov A. Y., Kemenova V. A., Rombaut P., Van den Mooter G. Eudragit® E PO as a complementary material for designing oral drug delivery systems with controlled release properties: comparative evaluation of new interpolyelectrolyte complexes with countercharged Eudragit® L 100 copolymers. Molecular Pharmaceutics. 2013; 10(7): 2630–2641. DOI: 10.1021/mp4000635.
М.П. Киселева, З.С. Шпрах, Л.М. Борисова и др. Доклиническое изучение противоопухолевой активности производного N-гликозида индолокарбазола ЛХС-1208. Сообщение I // Российский биотерапевтический журнал. 2015. № 2. С. 71-77.