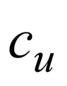Содержание:
- Потенциальная энергия при растяжении и сжатии
- Потенциальная энергия при растяжении и сжатии Внешние силы, действующие на тело, воздействуют на вызванные ими движения, и энергия деформации — потенциальная энергия накапливается в теле. Из-за накопленной энергии первоначальные размеры тела восстанавливаются при снятии нагрузки. Рассмотрим призму
стержня, растянутую силой P на величину AZ. В процессе нагружения балки сила медленно увеличивается от 0 до P, создавая работу L, численно равную потенциальной энергии деформации при упругой деформации: A = U. В процессе изменения силы вытягивания от 0 до P, тогда (рис. 38, а) дает силу P с несколькими значениями P,
равными AZb удлинения балки {приращение d P i тогда Удлинение является Людмила Фирмаль
основой силы, увеличенной на величину т / AZp dA = P jdAl i « Для риса. 38, б показана схема растяжения стержня, нагруженного при упругой деформации. На рисунке видно, что значение P1dAZ1 равно площади узкой заштрихованной полосы на диаграмме. дА-DQ, A = J dQ = Q. 41 задание (и, следовательно, потенциальная энергия) равно площади карты растяжения. Поскольку упругая деформация имеет треугольную форму, U = A = -RD1. (2.16) Подставляя здесь, вместо
внешней силы p, найдите внутреннюю силу n, равную ей, и относительное удлинение согласно уравнению (2.8) (2,17) N4 2. ‘ U = Рис 38А а), 2Z /////// Z Поскольку потенциальная энергия пропорциональна квадрату внутренней продольной силы, она всегда положительна. При расчете по функции нелинейности (2.17) невозможно использовать принцип независимости действия силы. Прямым уравнением (2.17) можно определить потенциальную энергию только для стержня постоянного сечения с постоянной
- продольной силой n на длине стержня. Если площадь поперечного сечения или продольная сила изменяется под воздействием луча, потенциальная энергия области с постоянными N и F при этих значениях резко изменяется: (2,18) Согласно некоторым законам, если поперечное или продольное усилие постепенно изменяется вдоль длины стержня, это должно быть записано: 42 — потенциальная энергия бесконечно малого сегмента стержня длиной dx, в течение которого поперечное сечение и внутренняя сила могут считаться
постоянными: N2dx dU = x, 2 £ FX Далее, интегрируйте это выражение по длине полосы: 1p N2dx (/ =. (2.19) 2J EFx ноль Рассмотрим пример определения потенциальной энергии. а) ‘^ 2’4X442. C A = 1 мкг Рис 39А Участок N P R I m e R1. Определить потенциальную энергию медного шагового луча. 39, а, с двумя концентрационными способностями -2 тонны и P2 = 5 т. Модуль упругости материала балки E = 10E кг! На рисунке показана диаграмма продольной силы. 39,6 Примените формулу (2.18) к графику, и вы увидите N2l2N2l3 2EFt + 2 £ F2 + 2EF2 + 20092-30 2-10G-5 20002-20 2-IO6-10 (-3000) М0 2-10G-10 = 34K.G-CM. P p и me p2. Рассчитать потенциальную энергию пучка и его поперечное сечение по линейному закону (рис. 40).
Из-за действия одной концентрирующей силы P продольная направленная сила внутри рассматриваемого пучка является внешней силой. И N = П. Сечение Людмила Фирмаль
на расстоянии х от правого конца 43 балки L / + (^ 2-L) l- один Примените формулу (2.19), и вы увидите Рис 40А Некоторые проблемы используют определенные концепции потенциальной энергии. Это относится к энергии, назначенной единицам начального объема пучка. Это не зависит от размера луча: = JJ_ = 2 _ U ~ Vo ~ Fo / O С тех пор но D / Это один Я — А Е.2 (2.20) Представление относительной деформации из-за напряжения по закону Гука Broadcast
Смотрите также:
- Учебник по сопротивлению материалов: сопромату
3.9. Потенциальная энергия деформации при осевом растяжении и сжатии
Потенциальной энергиейназывается энергия, накапливаемая в образце при его упругих деформациях. Потенциальная энергия численно равняется работе внешних сил, приложенных к телу, на вызванных ими перемещениях. За счет потенциальной энергии восстанавливаются первоначальная форма и размеры образца при снятии нагрузки.
Рассмотрим стержень, растянутый силой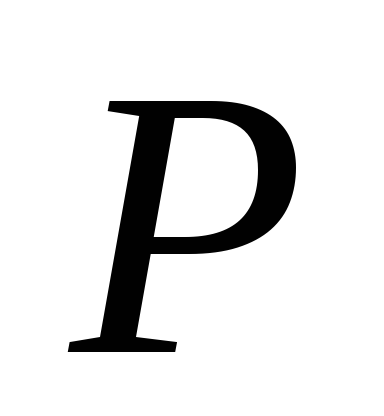 
на величину
. Растягивающая сила в процессе деформации медленно росла от 0 до
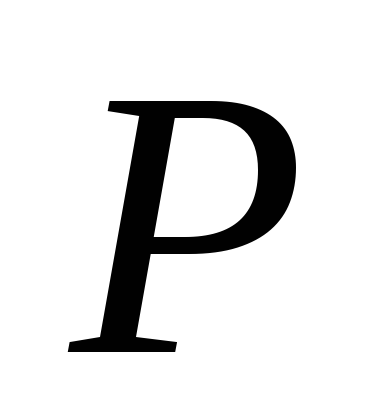и совершала работу, которая в переделах упругих деформаций численно равняется потенциальной энергии деформации:
.
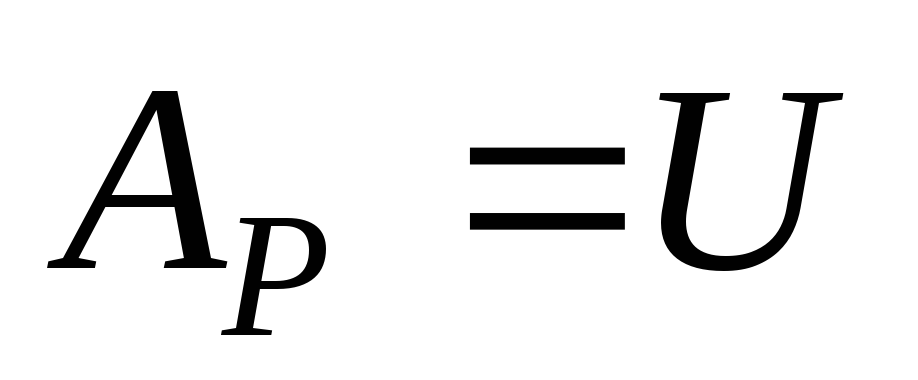Пусть в процессе деформации сила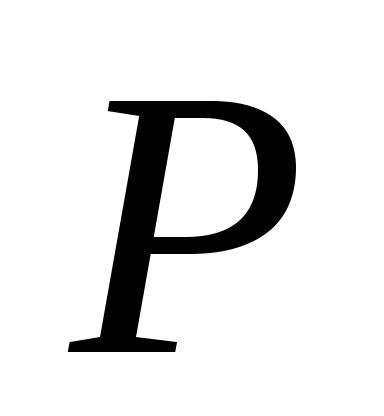 
приняла некоторое значение
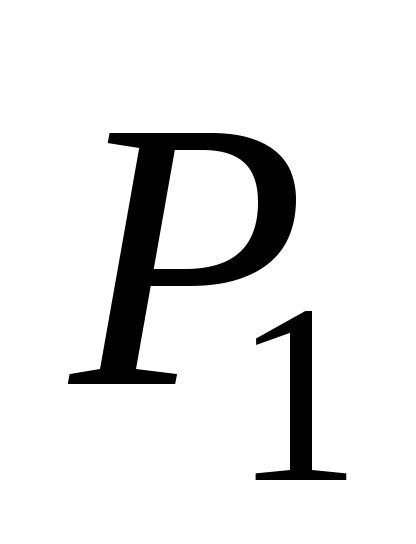. При этом удлинение стержня стало равным
(Рис.3.15,а). Дадим силе
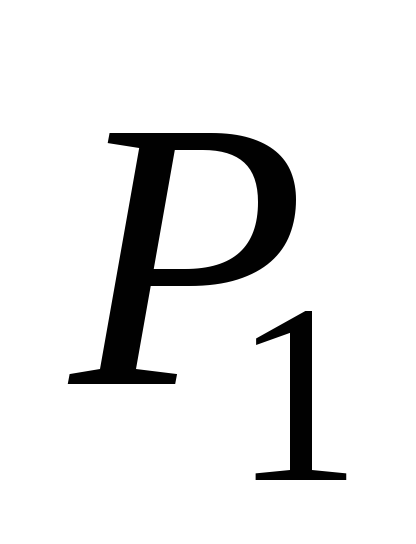приращение
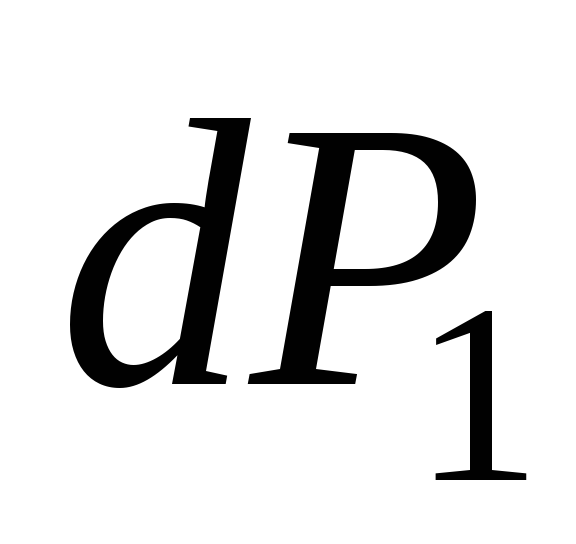, тогда удлинение вырастет на величину
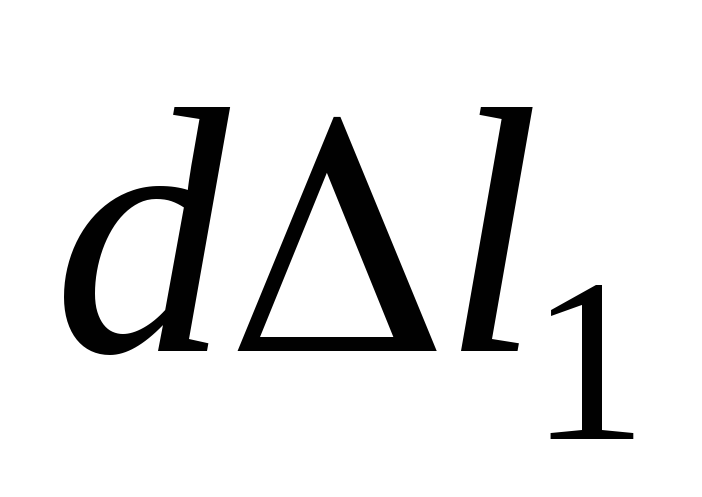. Элементарная работа силы
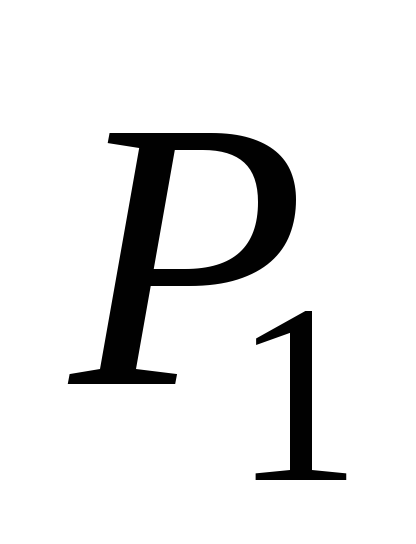на этом преремещении будет равна:
.
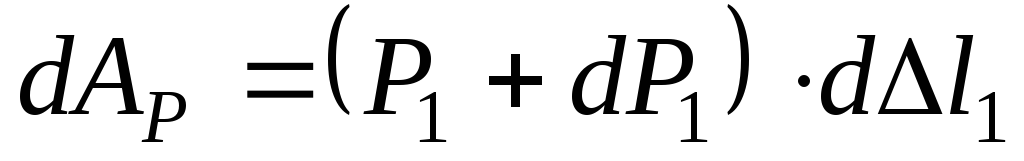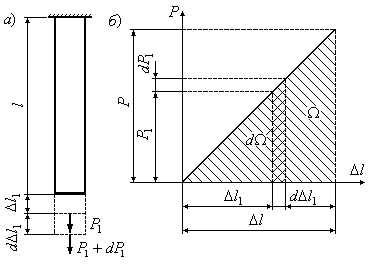
Рис.3.15
Пренебрегая величиной второго порядка малости выражение для элементарной работы получаем в виде:
.
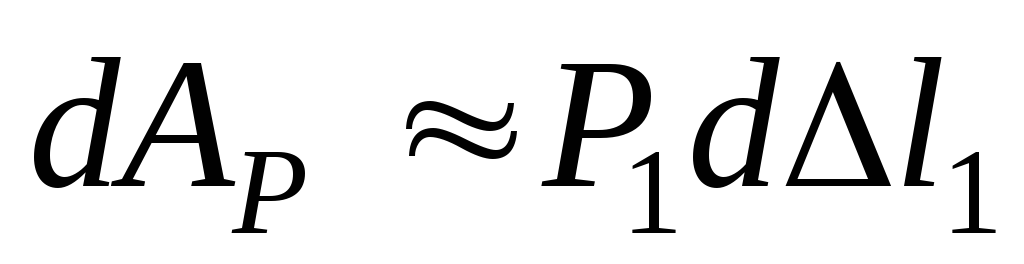На рис.3.15,б приведена диаграмма растяжения стержня в зоне упругих деформаций. Из рисунка видно, что величина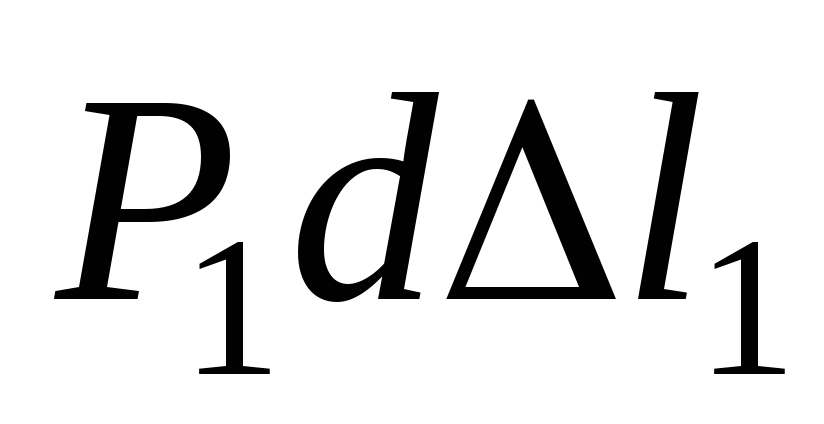 
равна площади узкой заштрихованной полоски диаграммы:
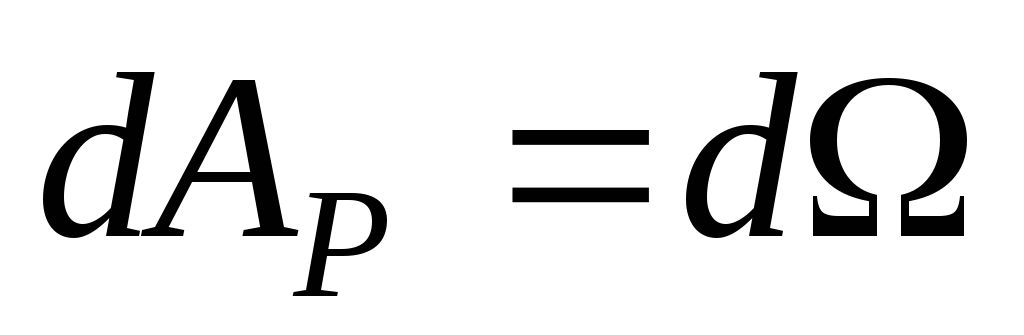. (3.17)
Всю работу на упругой деформации вычислим, проинтегрировав выражение (3.17) по всей площади диаграммы:
.
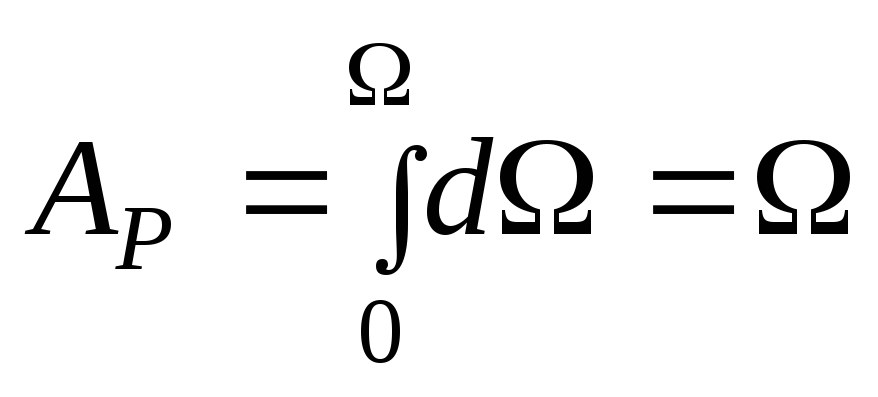Таким образом, работа и, следовательно, потенциальная энергия равны площади диаграммы растяжения, которая в пределах упругих деформаций имеет вид треугольника:
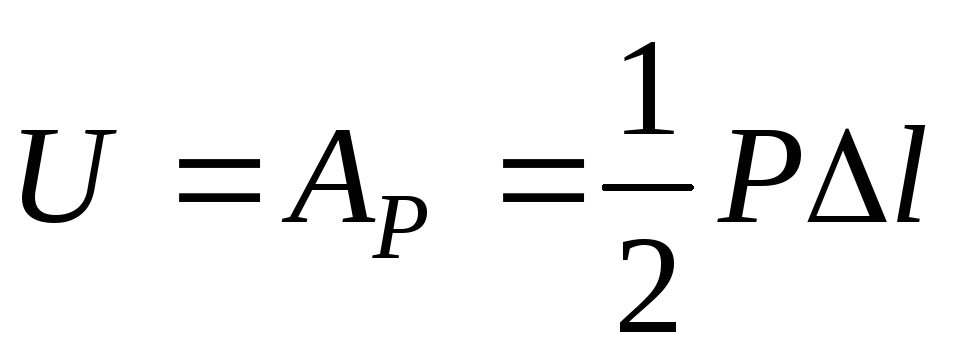. (3.18)
Подставляя в формулу (3.18) вместо силы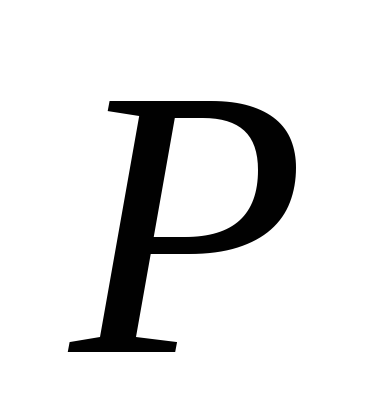 
равное ей внутреннее усилие
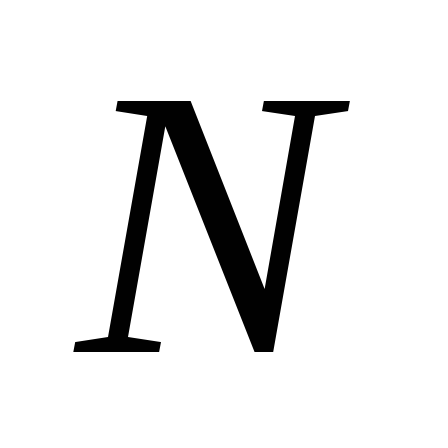и удлинение (3.7), получим:
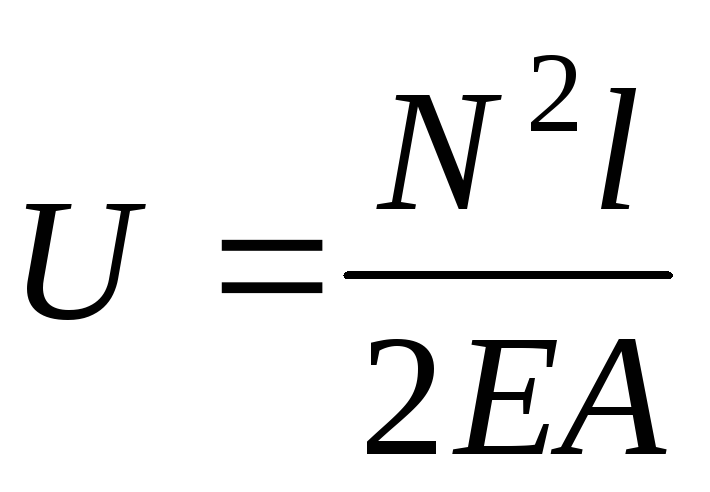. (3.19)
Анализируя выражение (3.19), приходим к выводу, что потенциальная энергия всегда будет положительной. Вследствие нелинейности функции (3.19) при вычислении потенциальной энергии нельзя пользоваться принципом независимости действия сил. Непосредственно выражением (3.19) можно пользоваться для вычисления потенциальной энергии лишь в том случае, если продольная сила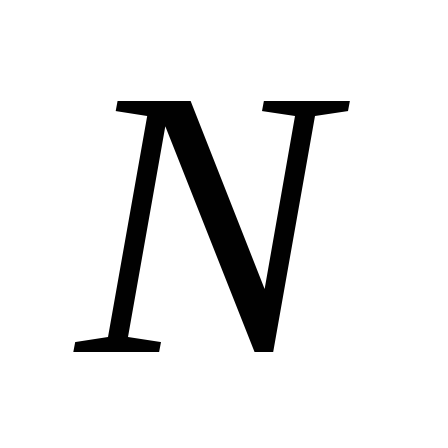 
на участке будет иметь постоянное значение. Если же площади поперечного сечения и продольные силы на участках стержня будут разными, то при скачкообразном изменении этих величин потенциальную энергию вычисляют на каждом участке отдельно, а результаты подсчетов складывают:
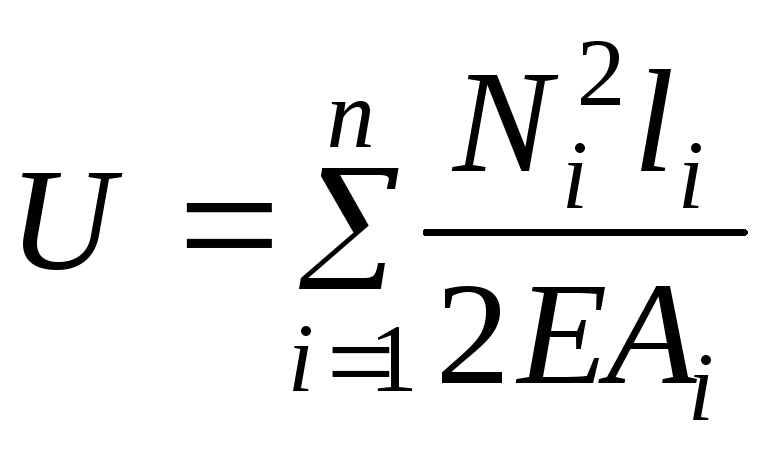. (3.20)
Если же площадь поперечного сечения или продольное усилие меняются по длине постепенно в соответствии с каким-либо законом, то сначала записывают выражение для потенциальной энергии бесконечно малого отрезка стержня длиной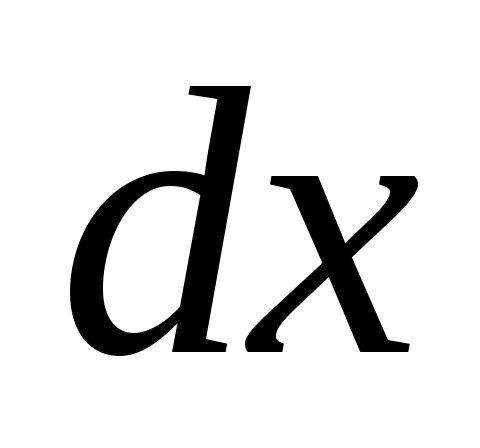 
, на протяжении которого и площадь поперечного сечения и продольное усилие могут считаться постоянными:
,
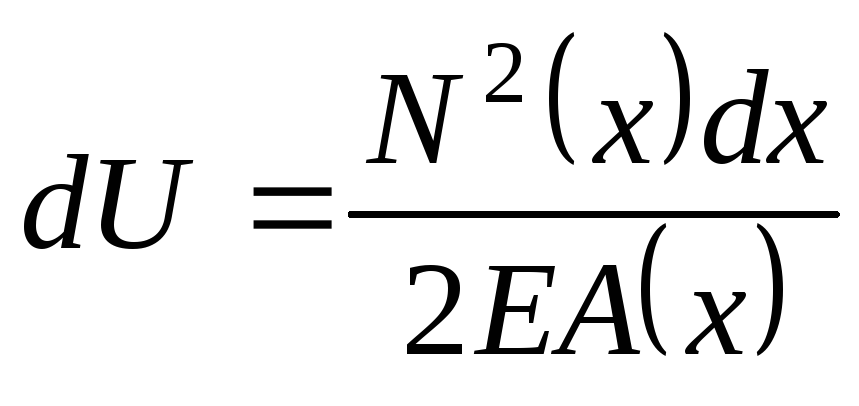а затем интегрируют это выражение по длине стержня. Тогда вся потенциальная энергия, накапливаемая в стержне, будет равна:
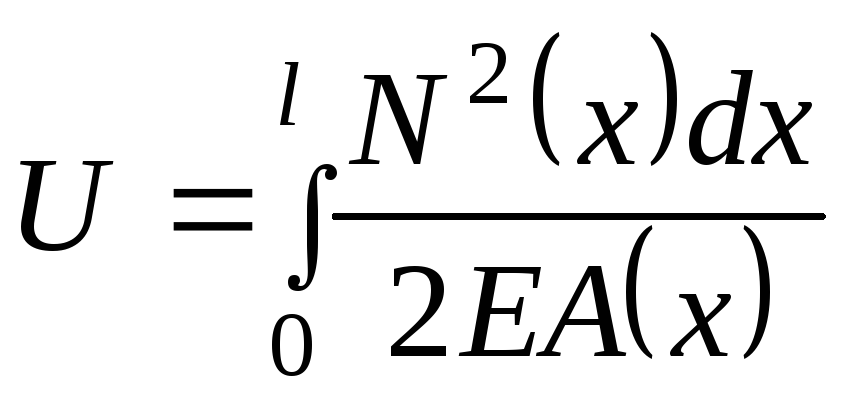. (3.21)
Энергия, затраченная на деформацию единицы объема материала в пределах упругости, называется удельной потенциальной энергиейи обозначается буквой
. Для стержня, растягиваемого силой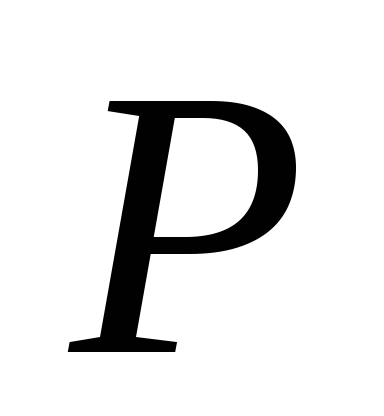
(Рис.3.15,а), удельная потенциальная энергия равна:
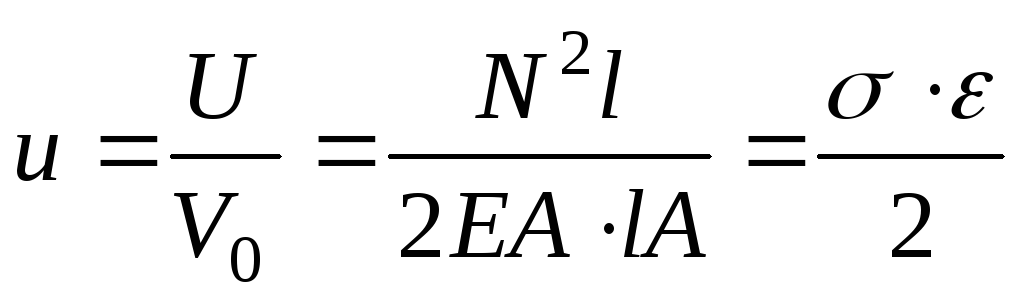, (3.22)
где 
объем образца перед началом нагружения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Техническая механика
Сопротивление материалов
Деформации при растяжении и сжатии
Продольные деформации при растяжении и сжатии
Характер деформаций, которым подвергается прямой брус при растяжении или сжатии мы определили, проведя опыт с резиновым брусом, на котором была нанесена сетка линий.
Теперь представим себе брус постоянного сечения имеющий длину l, один из концов которого защемлен, а к свободному концу приложена растягивающая сила F. Под действием этой силы брус удлинится на некоторую величину Δl, которую назовем абсолютным удлинением бруса.
Отношение абсолютного удлинения Δl к первоначальной длине бруса l назовем относительным удлинением и обозначим ε:
ε = Δl / l
Относительное удлинение — величина безразмерная, иногда его выражают в процентах.
Итак, деформация бруса при растяжении и сжатии характеризуется абсолютным и относительным удлинением или укорочением.
***
Закон Гука при растяжении и сжатии
Напряжения и деформации при растяжении и сжатии связаны между собой линейной зависимостью, которая называется законом Гука, по имени английского физика Р. Гука (1653-1703 г.г.), установившего этот закон.
Сформулировать закон Гука можно так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению.
Математически эта зависимость записывается так:
σ = E ε.
Здесь Е — коэффициент пропорциональности, который характеризует жесткость материала бруса, т. е. его способность сопротивляться деформации; его называют модулем продольной упругости, или модулем упругости первого рода.
Модуль упругости, как и напряжение, выражаются в паскалях (Па).
Значения Е для различных материалов устанавливаются экспериментально-опытным путем, и их величину можно найти в соответствующих справочниках.
Так, для стали Е = (1,96.…2,16) х 105 МПа, для меди Е = (1,00…1,30) х 105 МПа и т. д.
Следует оговориться, что закон Гука справедлив лишь в определенных пределах нагружения.
Если в формулу закона Гука подставить полученные ранее значения относительного удлинения и напряжения: ε = Δl / l , σ = N / А, то можно получить следующую зависимость:
Δl = Nl / (EА).
Произведение модуля упругости на площадь сечения Е×А, стоящее в знаменателе, называют жесткостью сечения при растяжении и сжатии; оно характеризует одновременно и физико-механические свойства материала бруса и геометрические размеры поперечного сечения этого бруса.
Приведенную выше формулу можно читать так: абсолютное удлинение или укорочение бруса прямо пропорционально продольной силе и длине бруса, и обратно пропорционально жесткости сечения бруса.
Выражение ЕА / l называют жесткостью бруса при растяжении и сжатии.
Приведенные выше формулы закона Гука справедливы лишь для брусьев и их участков, имеющих постоянное поперечное сечение, изготовленных из одного материала и при постоянной силе. Для бруса, имеющего несколько участков, отличающихся материалом, размерами сечения, продольной силой, изменение длины всего бруса определяется, как алгебраическая сумма удлинений или укорочений отдельных участков:
Δl = Σ (Δli)
***
Поперечные деформации при растяжении и сжатии
Описанный ранее опыт с резиновым брусом, на котором нанесена сетка линий, показал, что при растяжении поперечные размеры бруса уменьшаются, а при сжатии — увеличиваются, т. е. брус становится либо тоньше, либо толще. Это явление характерно для брусьев, изготовленных из всех материалов.
Опытным путем установлено, что при одноосном растяжении или сжатии отношение относительных поперечной и продольной деформаций для данного материала — величина постоянная.
Впервые на эту зависимость указал французский ученый С. Пуассон (1781-1840 г.г.) и математически она записывается так:
|ε1| = ν |ε|,
где ν — коэффициент поперечной деформации, называемый коэффициентом Пуассона.
Коэффициент Пуассона является безразмерной величиной, и характеризует упругие свойства материала. При растяжении и сжатии этот коэффициент принимается одинаковым.
Значения коэффициента Пуассона для разных материалов установлены опытным путем и их величины можно найти в соответствующих справочниках.
***
Потенциальная энергия деформации при растяжении
При статическом (медленном) растяжении образца растягивающая сила F возрастает от нуля до какого-то значения, удлиняет образец на величину Δl и при этом совершает работу W.
Эта работа аккумулируется в деформируемом образце в виде потенциальной энергии деформации U, причем, пренебрегая незначительными потерями энергии (например, тепловыми), можно считать, что W = U.
Путем изучения диаграмм растяжения образцов, установлено, что потенциальная энергия упругой деформации стержня длиной l постоянного поперечного сечения А при одинаковой во всех сечениях продольной силе N = F будет равна:
U = W = F Δl / 2 = N2 l / (2E А)
Сопротивление материалов оперирует, также, таким понятием, как удельная потенциальная энергия деформации, которая подсчитывается, как потенциальная энергия, приходящаяся на единицу объема бруса.
При одновременном действии растягивающих и сжимающих нагрузок или ступенчатом изменении размеров поперечного сечения бруса, его разбивают на однородные участки и для каждого подсчитывают потенциальную энергию деформации. Потенциальную энергию деформации всего бруса определяют, как сумму потенциальных энергий отдельных участков.
Анализируя формулу потенциальной энергии деформации можно сделать вывод, что эта величина всегда положительная, поскольку в ее выражения входят квадраты линейных и силовых величин. По этой причине при вычислении потенциальной энергии деформации нельзя применять принцип независимости действия сил (поскольку квадрат суммы не равен сумме квадратов слагаемых).
Единицей измерения потенциальной энергии деформации, как и работы, является джоуль (Дж).
***
Материалы раздела «Растяжение и сжатие»:
- Основные понятия о деформации растяжения и сжатия.
- Расчеты на прочность при растяжении и сжатии. Статически неопределимые задачи.
Смятие
Правильные ответы на вопросы Теста № 5
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Правильный вариант ответа | 3 | 3 | 1 | 2 | 1 | 3 | 2 | 2 | 1 | 1 |
Потенциальная энергия деформации при растяжении
Мы поможем в написании ваших работ! Мы поможем в написании ваших работ! Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? | При статическом (медленном) растяжении образца растягивающая сила F возрастает от нуля до какого-то значения, удлиняет образец на величину Δl и при этом совершает работу W. Эта работа аккумулируется в деформируемом образце в виде потенциальной энергии деформации U, причем, пренебрегая незначительными потерями энергии (например, тепловыми), можно считать, чтоW = U. Путем изучения диаграмм растяжения образцов, установлено, что потенциальная энергия упругой деформации стержня длиной l постоянного поперечного сечения А при одинаковой во всех сечениях продольной силе N = F будет равна: U = W = F Δl / 2 = N2l / (2E А) Сопротивление материалов оперирует, также, таким понятием, как удельная потенциальная энергия деформации, которая подсчитывается, как потенциальная энергия, приходящаяся на единицу объема бруса. При одновременном действии растягивающих и сжимающих нагрузок или ступенчатом изменении размеров поперечного сечения бруса, его разбивают на однородные участки и для каждого подсчитывают потенциальную энергию деформации. Потенциальную энергию деформации всего бруса определяют, как сумму потенциальных энергий отдельных участков. Анализируя формулу потенциальной энергии деформации можно сделать вывод, что эта величина всегда положительная, поскольку в ее выражения входят квадраты линейных и силовых величин. По этой причине при вычислении потенциальной энергии деформации нельзя применять принцип независимости действия сил (поскольку квадрат суммы не равен сумме квадратов слагаемых). Единицей измерения потенциальной энергии деформации, как и работы, является джоуль (Дж). Геометрические характеристики плоских сечений При некоторых видах деформаций прочность и жесткость (способность противостоять деформации) элементов конструкций зависит не только от величины поперечного сечения, но и от формы этого сечения. Самый простой пример — обыкновенную школьную линейку можно легко изогнуть относительно широкой стороны поперечного сечения и совершенно невозможно изогнуть относительно его короткой стороны. При этом общая площадь сечения в обоих случаях одинакова. На основании этого примера становится очевидным, что на сопротивление некоторым видам деформации оказывает влияние (иногда — решающее) не только величина площади сечения бруса, но и его геометрическая форма. При изучении деформаций изгиба и кручения нам потребуется знание некоторых геометрических характеристик плоских сечений, которые оказывают влияние на способность конструкций сопротивляться деформациям относительно той или иной оси либо полюса (точки). Чтобы понять суть явления и влияния этих геометрических характеристик на сопротивление бруса, например, изгибу, следует обратиться к основополагающим постулатам сопромата. Как известно из установленного в 1660 году английским физиком Робертом Гуком закона, напряжение в сечениях бруса прямо пропорционально его относительному удлинению. Очевидно, что волокна, расположенные дальше от оси изгиба, растягиваются (или сжимаются) сильнее, чем расположенные вблизи оси. Следовательно, и напряжения возникающие в них будут бόльшими. Можно привести условную сравнительную аналогию между напряжением в разных точках сечения бруса с моментом силы — чем больше плечо силы — тем больше ее момент (относительно оси или точки). Аналогично — чем дальше от какого-либо полюса (оси) отстоит точка в сечении, тем большее напряжение в ней возникает при попытке изогнуть или скрутить брус относительно этого полюса (оси). *** Статический момент площади Статическим моментом площади плоской фигуры относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений элементарных площадок на расстояния от них до этой оси. Статический момент площади плоской фигуры обозначают S с индексом оси, относительно которой он рассматривается: Sx,Sy,Sz. Sx= Σ y dA; Sy= Σ x dA. Анализ этих формул позволяет сделать вывод, что статический момент площади фигуры относительно оси, лежащей в этой же плоскости, равен произведению площади фигуры на расстояние от ее центра тяжести до этой оси. Единица измерения статического момента площади — метр кубический (м3). При определении статического момента площади сложной фигуры можно применять метод разбиения, т. е. определять статический момент всей фигуры, как алгебраическую сумму статических моментов отдельных ее частей. При этом сложная геометрическая фигура разбивается на простые по форме составные части — прямоугольники, треугольники, окружности, дуги и т. п., затем для каждой из этих простых фигур подсчитывается статический момент площади, и определяется алгебраическая сумма этих моментов. *** Полярный момент инерции Полярным моментом инерции плоской фигуры относительно полюса (точки), лежащего в той же плоскости, называется сумма произведений элементарных площадок этой фигуры на квадрат их расстояний до полюса. Полярный момент инерции обозначают Iρ , а формула для его определения записывается так: Iρ= Σ ρ2dA. Единица измерений полярного момента инерции — м4, из чего следует, что он не может быть отрицательным. Понятие полярного момента инерции понадобится при изучении деформаций кручения круглых валов, поэтому приведем формулы для определения полярного момента квадратного, круглого и кольцевого сечения.
Очевидно, что полярный момент инерции кольцевого сечения равен разности полярных моментов инерции большого и малого кругов, ограничивающих это сечение. *** Осевой момент инерции Осевым моментом инерции плоской фигуры относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений площадей элементарных площадок на квадрат расстояний от них до этой оси (рис). Осевой момент инерции обозначается I с индексом, соответствующим оси: Ix= Σ y2dA; Iy= Σ x2dA. Если при этом площадь элементарных площадок принять стремящимися к минимуму, то можно использовать методы интегрального исчисления, заменив знак суммы Σ на знак интеграла ∫. Очевидно, что осевой и полярный момент инерции выражаются в одинаковых единицах — м4. Осевой момент инерции величина всегда положительная и не равна нулю (м4 не может быть отрицательным, а площадь не может быть равной нулю, иначе пропадает и сама фигура, как площадка). Если сложить осевые моменты инерции плоской фигуры относительно перпендикулярных осей, то получим полярный момент инерции этой фигуры относительно точки пересечения этих осей (начала координат), т. е. : Ix+ Iy= Iρ. Так как интеграл суммы равен сумме интегралов, то момент инерции сложной фигуры можно вычислить как сумму моментов инерции простых фигур, на которые разбивают сложную фигуру. Понятие осевого момента инерции понадобится при изучении теории изгиба. Приведем формулы для определения осевых моментов инерции наиболее часто встречающихся при расчетах форм сечений:
*** |
- ОФС.1.2.1.1.0003.15 Спектрофотометрия в ультрафиолетовой и видимой областях // Государственная фармакопея, XIII изд.
- Харенко Е. А., Ларионова Н. И., Демина Н. Б. Мукоадгезивные лекарственные формы. Химико-фармацевтический журнал. 2009; 43(4): 21–29. DOI: 10.30906/0023-1134-2009-43-4-21-29.
- ОФС.1.2.1.2.0003.15 Тонкослойная хроматография // Государственная фармакопея, XIII изд.
- https://lfirmal.com/potencialnaya-ehnergiya-pri-rastyazhenii-i-szhatii/.
- https://studfile.net/preview/5397441/page:8/.
- https://k-a-t.ru/tex_mex/1-sopromat_rastyajen2/.
- https://infopedia.su/2x8f68.html.
- Киржанова Е. А., Хуторянский В. В., Балабушевич Н. Г., Харенко А. В., Демина Н. Б. Методы анализа мукоадгезии: от фундаментальных исследований к практическому применению в разработке лекарственных форм. Разработка и регистрация лекарственных средств. 2014; 3(8): 66–80. DOI: 10.33380/2305-2066-2019-8-4-27-31.
- Puccinotti, «Storia della medicina» (Ливорно, 1954—1959).
