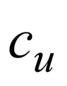Сопромат.in.ua: Центральное растяжение-сжатие. Определение усилий

Растяжение (сжатие) — это такой вид нагружения стержня, при котором в его поперечном сечении возникает внутренняя продольная сила Ν, действующая вдоль центральной оси z.

Продольная сила Ν — это равнодействующая всех внутренних нормальных сил в сечении. Для вычисления продольной силы применяется метод сечений.

2014-09-07 19-04-45 Скриншот экрана

Продольная сила Ν численно равна алгебраической сумме проекций всех сил, действующих по одну сторону от рассматриваемого сечения, на продольную ось бруса.

Правило знаков для продольной силы Ν: при растяжении продольная сила положительна, при сжатии — отрицательна.

2014-09-07 19-09-39 Скриншот экрана

График изменения продольных сил по длине стержня называется эпюрой. Эпюра N строится методом сечений на характерных участках бруса. Строится эпюра для использования ее при расчете бруса на прочность. Она дает возможность найти наибольшие значения продольных сил и положение сечений, в которых они возникают.

При растяжении (сжатии) возникают только нормальные напряжения. Согласно гипотезе Я. Бернулли (или гипотеза плоских сечений) в поперечных сечениях, удаленных от места приложения нагрузок, нормальные напряжения распределяются по сечению практически равномерно, а сами сечения, перпендикулярные к оси стержня z, остаются плоскими в процессе нагружения.

Нормальные напряжения в сечении при растяжении (сжатии) вычисляются по формуле

где А — площадь поперечного сечения.

Правило знаков для σ совпадает с правилом знаков для N.

В наклонном сечении, нормаль к которому составляет угол α с осью стержня z,

При растяжении в продольном направлении стержень удлиняется, а его поперечные размеры уменьшаются, при сжатии, напротив, в продольном направлении стержень укорачивается, а его поперечные размеры увеличиваются; Δℓ — абсолютное удлинение или укорочение участка стержня длиной ℓ, Δb — абсолютная поперечная деформация.

Относительное удлинение или укорочение участка стержня длиной ℓ, называемое линейной деформацией, определяется следующим образом

ε=Δℓ/ℓ.

Экспериментально установлено, что в определенной области нагрузок при упругом поведении материала между нормальными напряжениями и линейными деформациями существует линейная зависимость (закон Гука для напряжений)

σ=εЕ,

где Е — модуль продольной упругости или модуль Юнга, это физическая const. Для каждого из материалов величина модуля упругости имеет свое значение:

сталь, Е = 2.105 МПа,

медь, Е = 1.105 МПа,

алюминий, Е = 0,7.105 МПа.

Значение модуля упругости устанавливается экспериментально.

Согласно закону Гука (данную запись называют законом Гука для деформаций)

Δℓ=Νℓ/ЕА

Произведение ЕА — называется жесткостью стержня при растяжении — сжатии.

Перемещение произвольного сечения ступенчатого стержня

w=∑Δℓi

Относительная поперечная деформация:

ε′=Δb/b

где b — поперечный размер стержня.

Эксперименты также показывают, что в упругой стадии деформирования между продольной и поперечной деформациями существует взаимосвязь

μ =│ε′⁄ε│ — const,

где μ — коэффициент Пуассона, берется по модулю ,поскольку у продольной и поперечной деформации разные знаки (при растяжении продольные волокна увеличиваются, а поперечные уменьшаются в размере).

Для твердых материалов имеет значения коэффициент Пуассона

0≤μ ≤0,5

Изменение температуры стержня вызывает его удлинение (при нагревании) или укорочение (при охлаждении)

2014-09-01 22-02-54 Скриншот экрана

где — a- коэффициент линейного температурного расширения; Δtº=(tºк-tºн) — изменение температуры между значениями начальным (tºн) и конечным (tºк).

Статически неопределимыми называют системы, имеющие лишние связи — внешние или внутренние.

Для определения внутренних усилий в таких системах недостаточно рассматривать только уравнения равновесия.

В этом случае требуются дополнительные уравнения, число которых равно количеству лишних связей. Дополнительные уравнения составляются на основе анализа картины деформирования системы и использования законов деформирования ее элементов.

Алгоритм решения подобных задач включает следующее:

1) Статическая часть. Составляются уравнения равновесия с включением неизвестных усилий, действующих по направлению лишних связей.

2) Геометрическая часть. Составляются уравнения, описывающие взаимосвязь перемещений характерных точек, удлинений и укорочений отдельных стержней между собой.

3) Физическая связь. Записываются законы деформирования отдельных стержней системы.

Порядок расчета статически неопределимых брусьев

Задаться направлениями возможных опорных реакций и составить уравнение статики для всей системы в целом.
Определить степень статической неопределимости и использовать метод сечений с целью выразить неизвестные усилия через неизвестные опорные реакции. При этом неизвестные продольные силы (N) следует предполагать положительными и поэтому направлять «от сечения».
Сформулировать условие совместности деформаций участков бруса.
В процессе превращения условия совместности в уравнение совместности деформаций различий в характере деформаций участков не учитывать.

Порядок расчета статически неопределимых шарнирно-стержневых систем

Задаться направлениями опорных реакций, но уравнений равновесия для всей системы не составлять, а сразу использовать метод сечений и составить уравнения статики для выделенной части системы.
Определить степень статической неопределимости как разницу между количеством всех неизвестных, оказавшихся в уравнениях статики, и числом самих этих уравнений.
Рассмотреть (изобразить) любую возможную картину деформаций системы и из ее анализа сформулировать условия совместности деформаций стержней системы (столько, какова степень статической неопределимости).
В процессе преобразования условий совместности в уравнения совместности деформаций обязательно учитывать различие в характере деформаций стержней (т.е. вводить удлинение со знаком «плюс», а укорочение со знаком «минус») в соответствии с той картиной деформации, которую мы рассматриваем.

Содержание

Сопромат.in.ua

Центральным растяжением (или центральным сжатием) называется такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила (растягивающая или сжимающая), а все остальные внутренние усилия равны нулю. Иногда центральное растяжение (или центральное сжатие) кратко называют растяжением (или сжатием) .

Правило знаков Растягивающие продольные усилия принято считать положительными, а сжимающие — отрицательными.

Рассмотрим прямолинейный брус (стержень), нагруженный силой F

Растяжение стержня

Определим внутренние усилия в поперечных сечениях стержня методом сечения.

Напряжение — это внутренне усилие N, приходящее на единицу площади A. Формула для нормальных напряжений σ при растяжении

$$sigma = frac{N}{A} $$

Так как поперечная сила при центральном растяжении-сжатии равна нулю, то и касательное напряжение [math]tau=0[/math].

Условие прочности при растяжении-сжатии

$$ max; sigma = {Biggvertfrac{N}{A}Biggvert} leq [sigma] $$

Дифференциальная зависимость внутренних усилий от распределенной нагрузки:

dN =q·dx

Определение внутренних усилий и напряжений

Рассмотрим вариант определения внутренних сил под действием произвольных сосредоточенных и распределенных сил, направленных вдоль стержня.

Продольное усилие N равняется сумме сил (сосредоточенных Fi и распределенных qi), расположенных по одну сторону от рассматриваемого сечения.

Общая формула для определения продольного усилия в произвольном сечении

$$N(x)=sum F _i + sum int q _i(x)cdot dx $$

Примем, что распределенная нагрузка постоянная. Тогда можно записать

$$N(x)=sum F _i + sum t q _i(x)cdot(x-L _{q _{i}н}) — sum t q _i(x)cdot(x-L _{q _{i}k}),$$

где Lqiн и Lqiк — расстояние от начала координат до начала и конца распределенной силы qi

Для эпюр продольных сил характерны определенные закономерности, знание которых позволяет оценить правильность выполненных построений.

Эпюры N всегда прямолинейные.
На участке, где нет распределенной нагрузки, эпюра N — прямая, параллельная оси; а на участке под распределенной нагрузкой — наклонная прямая.
Под точкой приложения внешней сосредоточенной силы на эпюре обязательно должен быть скачок (разрыв первого рода) на величину этой силы.

Правильность построения эпюры обеспечивается также надлежащим выбором так называемых характерных сечений, то есть тех сечений, в которых величина внутренней силы обязательно должна быть определена. К характерным сечениям относятся:

сечения, расположенные бесконечно близко по обе стороны от точек приложения сосредоточенных сил и моментов;
сечения, расположенные в начале и в конце каждого участка с распределенной нагрузкой;
сечения, расположенные бесконечно близко к опорам, а также на свободных концах.

Пример определения продольных усилий

Пусть стержень длиной L=15 нагружен двумя сосредоточенными растягивающими силами F1=7 в точке FL1=14 и F2=2 в точке FL2=6. Стержень загружен сжимающей распределенной силой q=-1.2, приложенной от начала стержня до Lq1=12. Нужно построить эпюру продольных усилий.

Для определения усилий воспользуемся пакетом SciLab ( см. также здесь).

Создадим две маленькие функции и запишем их в файл n_calc.sce

[N]=Nx_calc(x,q,F) // определение суммы всех сил справа от сечения x Fsum=0; r=size(F,’r’); for i=1:r Fsum=Fsum+F(i,2)*(x<F(i,1)); end; q_sum=0; r=size(q,’r’); for i=1:r q_sum=q_sum+q(i,3)*(x-q(i,1))*(x<q(i,1))-q(i,3)*(x-q(i,2))*(x<q(i,2)); end; N=Fsum+q_sum; end //—- [x,y]=N_calc(q,F,L,step) // формирования таблицы усилий в стержне с шагом step x=[0:step:L,F(:,1)’] // знак ‘ — транспонирование матрицы x=gsort(x,’g’,’i’); y=[]; for i=1:length(x) y(i)=Nx_calc(x(i),q,F); end end

Задаем начальные условия и строим эпюру продольных сил

// подключение нашей функции exec(‘n_calc.sce’) // распределенная нагрузка [начало,конец, интенсивность нагрузки] q=[0, 12, -1.2]; // сосредоточенная нагрузка [точка приложения, значение силы] F=[14, 4; 6, 2]; // Длина L=15; // шаг задаем очень маленьким step=0.1; // вычисление [x,y]=N_calc(q,F,L,step); // построение эпюры plot2d(x,y) plot2d3(x,y) xgrid(3);

С помощью функции Nx_calc можно определить усилие N в любом сечении x.

Так как Scilab, GNU Octave и MATLAB имеют очень близкие языки, то для решения этой задачи в этих пакетах можно воспользоваться выше приведенным алгоритмом.

2й вариант

Приведем еще один вариант определения продольных усилий при центральном растяжении-сжатии с помощью языка программирования R.

# Центральное растяжение-сжатие # # определение суммы всех сил справа от сечения Xi Nx_calc <- (Xi,q,aF) { Nsum <- (Fx, x) {N<-Fx[2]*(x<=Fx[1]);} Fsum<-sum(apply(aF,1, Nsum, x=Xi)); q_sum <- (qx,x) {N<-qx[3]*(x-qx[1])*(x<=qx[1])-qx[3]*(x-qx[2])*(x<=qx[2]); } qsum<-sum(apply(q,1, q_sum, x=Xi)); N<-Fsum+qsum; } # формирования таблицы усилий в стержне с шагом step # и отображение эпюры N_calc <- (q,F,L,step) { #превращаем вектор в матрицу Fi<-matrix(F,ncol=2,byrow=TRUE); dimnames(Fi)[[2]] <- c(‘x’,’F’); #проверяем результат (Fi); qi<-matrix(q,ncol=3,byrow=TRUE); dimnames(qi)[[2]] <- c(‘Ln’,’Lk’,’q’); (qi); x<- c(seq(from=0, to=L, by=step),Fi[,1]); x<-sort(x); y<- sapply(x,Nx_calc, q=qi, aF=Fi); # рисуем plot(x,y,type=»h»,ylab=»Усилие», col=»blue»,main=»Эпюра усилий N»); lines(x,y); abline(h=0); # добавим точки, где приложены силы xf<-Fi[,1]; yf<- sapply(xf,Nx_calc, q=qi, aF=Fi); points(xf,yf); text(xf,yf,yf,adj=1,pos=4); } # формирования таблицы усилий в стержне с шагом step # и отображение эпюры (Усовершенствованный вариант №2) N_calc2 <- (q,F,L) { #превращаем вектор в матрицу Fi<-matrix(F,ncol=2,byrow=TRUE); dimnames(Fi)[[2]] <- c(‘x’,’F’); #проверяем результат (‘Сосредоточенные силы Fi’);(Fi); qi<-matrix(q,ncol=3,byrow=TRUE); dimnames(qi)[[2]] <- c(‘Ln’,’Lk’,’q’); (‘Распределенные нагрузки’);(qi); z<-Fi[,1]; x1<-numeric(); eps=L/1000; # малая величина for ( i in 1:length(z) ) { x1<-c(x1,z[i]-eps,z[i],z[i]+eps) } x<- c(0,L,qi[,1],qi[,2],x1); x<-sort(x); y<- sapply(x,Nx_calc, q=qi, aF=Fi); # рисуем plot(x,y,type=»l»,ylab=»Усилие», main=»Эпюра усилий N», sub=’вариант №2′ ); abline(h=0); polygon(c(x,L,0),c(y,0,0),col=’gray’) # добавим точки, где приложены силы xf<-Fi[,1]; yf<- sapply(xf,Nx_calc, q=qi, aF=Fi); points(xf,yf); text(xf,yf,yf,adj=1,pos=4); # Определяем максимальное сжимающее и растягивающее усилие y_max<-max(y); y_min<-min(y); if ( y_max > 0 ) { x_max= x[which.max(y)]; (sprintf(«Максимальное растягивающее значение N=%f при x=%f»,y_max,x_max ) ); points(x_max,y_max, col=»red»); text(x_max,y_max,y_max,col=’blue’,pos=4); } if ( y_min < 0 ) { x_min= x[which.min(y)]; (sprintf(«Максимальное сжимающее значение N=%f при x=%f»,y_min,x[which.min(y)] ) ); points(x_min,y_min, col=»red»); text(x_min,y_min,y_min,col=’blue’,adj=1,pos=4); } } Исходный код функций

Ниже приведен сеанс построения эпюры N в R

> source(«N_calc.r», echo=TRUE); > # Центральное растяжение-сжатие > # > # определение суммы всех сил справа от сечения Xi > Nx_calc <- (Xi,q,aF) { + Nsum <- (Fx, …. [TRUNCATED] > # формирования таблицы усилий в стержне с шагом step > # и отображение эпюры > # > N_calc <- (q,F,L,step) { + #превращаем вектор в матри …. [TRUNCATED] > # формирования таблицы усилий в стержне с шагом step > # и отображение эпюры (Усовершенствованный вариант №2) > N_calc2 <- (q,F,L) { + # …. [TRUNCATED] > > L=15; # Длина > step=0.1; # шаг задаем очень маленьким > # распределенная нагрузка [начало,конец, интенсивность нагрузки] > q<-c(0, 12, -1.2); > # сосредоточенная нагрузка. Порядок заполнения [точка приложения, значение силы] … > F=c(14, 4, 6, 2); > N_calc2(q,F,L) [1] «Сосредоточенные силы Fi» x F [1,] 14 4 [2,] 6 2 [1] «Распределенные нагрузки» Ln Lk q [1,] 0 12 -1.2 [1] «Максимальное растягивающее значение N=4.000000 при x=12.000000» [1] «Максимальное сжимающее значение N=-8.400000 при x=0.000000» >

В результате на экране отобразится следующая эпюра:

Здесь сразу определены опасные сечения.

Так же, как и в предыдущем варианте, с помощью функции Nx_calc можно определить усилие N в любом сечении x.

Дополнительно

Пример из пособия МИИТ Эпюра продольных сил при центральном растяжении-сжатии (формат pdf).

—

Связанные статьи

Найти внутренние усилия и построить их эпюры для стержня
Закон Гука

метки: scilab, внутренние усилия, определение усилий: примеры, растяжение-сжатие, язык r

Задача. Определить напряжение в стальных стержнях, поддерживающих абсолютно жёсткую балку. Материал — сталь Ст3, α=60°, [σ]=160МПа.

Схему вычерчиваем в масштабе. Нумеруем стержни.

2019-01-02_13-56-14

В шарнирно-неподвижной опоре А возникают реакции RА и НА. В стержнях 1 и 2 возникают усилия N1 и N2. Применим метод сечений. Замкнутым разрезом вырежем среднюю часть системы. Жесткую балку покажем схематично — линией, усилия N1 и N2 направим от сечения.

2019-01-02_13-57-54

Составляем уравнения равновесия

2019-01-02_13-58-31

Количество неизвестных превышает количество уравнений статики на 1. Значит, система один раз статически неопределима, и для её решения потребуется одно дополнительное уравнение. Чтобы составить дополнительное уравнение, следует рассмотреть схему деформации системы. Шарнирно-неподвижная опора А остается на месте, а стержни деформируются под действием силы.

Схема деформаций

2019-01-02_13-59-28

По схеме деформаций составим условие совместности деформаций из рассмотрения подобия треугольников АСС1и АВВ1. Из подобия треугольников АВВ1 и АСС1 запишем соотношение:

, где ВВ1=Δℓ1 (удлинение первого стержня)

Теперь выразим СС1 через деформацию второго стержня. Укрупним фрагмент схемы.

2019-01-02_14-01-20

Из рисунка видно, что СС2 = СС1·cos (90º-α)= СС1·sinα.

Но СС2= Δℓ2 , тогда Δℓ2= СС1·sinα, откуда:

Превратим условие совместности деформации (4) в уравнение совместности деформации с помощью формулы Гука для деформаций. При этом обязательно учитываем характер деформаций (укорочение записываем со знаком «-», удлинение со знаком «+»).

2019-01-02_15-05-29

Тогда уравнение совместности деформаций будет:

Сокращаем обе части на Е, подставляем числовые значения и выражаем N1 через N2

2019-01-02_15-06-53

Подставим соотношение (6) в уравнение (3), откуда найдем:

N1 = 7,12кН (растянут),

N2 =-20,35кН (сжат).

Определим напряжения в стержнях.

2019-01-02_15-07-37

Задача решена.

Расчет бруса с зазором. Для статически неопределимого стального ступенчатого бруса построить эпюры продольных сил, нормальных напряжений, перемещений. Проверить прочность бруса. До нагружения между верхним концом и опорой имел место зазор Δ=0,1 мм. Материал — сталь Ст 3, модуль продольной упругости Е=2·105 МПа, допускаемое напряжение [σ]=160МПа.

2016-09-04 13-42-56 Скриншот экрана

После нагружения зазор закроется и реакции возникнут и в нижней, и в верхней опоре. Покажем их произвольно, это реакции RA и RВ. Составим уравнение статики.

∑у=0 RA — F1 + F2 — RВ=0

В уравнении 2 неизвестных, а уравнение одно, значит задача 1 раз статически неопределима, и для ее решения требуется 1 дополнительное уравнение.

Это уравнение совместности деформаций. В данном случае совместность деформаций участков бруса состоит в том, что изменение длины бруса (удлинение) не может превзойти величины зазора, т.е. Δℓ=Δ, это условие совместности деформации.

Теперь разобьем брус на участки и проведем на них сечения — их 4 по количеству характерных участков. Каждое сечение рассматриваем отдельно, двигаясь в одном направлении — от нижней опоры вверх. В каждом сечении выражаем силу N через неизвестную реакцию. Направляем N от сечения.

2016-09-04 13-54-16 Скриншот экрана

Выпишем отдельно значения продольных сил в сечениях:

N1 = — RА

N2 = 120 — RА

N3 = 120 — RА

N4 = 30- RА

3. Вернемся к составлению условия совместности деформации. Имеем 4 участка, значит

Δℓ1+ Δℓ2+ Δℓ3+ Δℓ4= Δ (величина зазора).

Используя формулу Гука для определения абсолютной деформации составим уравнение совместности деформаций, — это именно то дополнительное уравнение, которое необходимо для решения задачи.

Попробуем упростить уравнение. Помним, что величина зазора Δ=0,1 мм = 0,1·10-3 м

Е — модуль упругости, Е=2·105МПа=2·108кПа.

Подставляем вместо N их значения, записанные через опорную реакцию RА.

2016-09-04 14-06-23 Скриншот экрана

4. Вычисляем N и строим эпюру продольных сил.

N1=- RА=-47,5кН

N2=120 — RА=72,5кН

N3=120 — RА=72,5кН

N4=30- RА=-17,5кН.

2016-09-04 14-16-38 Скриншот экрана

5. Определяем нормальные напряжения σ по формуле и строим их эпюры

2016-09-04 14-20-31 Скриншот экрана

Строим эпюру нормальных напряжений.

2016-09-04 14-24-46 Скриншот экрана

Проверяем прочность.

σmax= 90,63 МПа < [σ]=160МПа.

Прочность обеспечена.

Вычисляем перемещения, используя формулу Гука для деформаций.

Идем от стены А к зазору.

2016-09-04 14-22-44 Скриншот экрана

Получили величину ω4, равную зазору ,это является проверкой правильности определения перемещений.

Строим эпюру перемещений.

2016-09-04 14-27-36 Скриншот экрана

Задача решена.

Для статически определимого стального ступенчатого бруса построить эпюры продольных сил, нормальных напряжений и перемещений. Проверить прочность бруса. Материал — сталь Ст 3, модуль продольной упругости Е=2·105 МПа, допускаемое напряжение [σ]=160МПа.

2016-09-04 11-49-14 Скриншот экрана

Произвольно направляем реакцию стены RAи определяем её из уравнения равновесия.

∑у=0 — RA+F3 — F2+ F1 =0

RA= F3 — F2+ F1 =60-25+10=45кН.

Определяем продольные силы N методом сечений. Сечение расставляем на характерных участках (между изменениями). Подсказкой может служить размерная нитка — сколько отсечено отрезков, столько будет и участков с сечениями. В нашей задаче их 6.Каждое сечение рассматриваем отдельно с любой стороны на наше усмотрение. Силу N направляем от сечения.

2016-09-04 12-42-47 Скриншот экрана

2016-09-04 12-43-33 Скриншот экрана

Строим эпюру N. Все значения откладываем перпендикулярно от нулевой линии в выбранном нами масштабе.

Положительные значения условимся откладывать вправо от нулевой линии, отрицательные — влево.

2016-09-04 12-22-12 Скриншот экрана

Определяем нормальные напряжения σ в сечениях по формуле . Внимательно смотрим, по какой площади проходит сечение.

2016-09-04 12-25-22 Скриншот экрана

Строим эпюру σ.

2019-10-03_22-46-50

Проверим прочность по условию прочности

|σmax|= 75 МПа < [σ]=160МПа.

Прочность обеспечена.

4. Определяем перемещение бруса.

Расчет ведется от стены, в которой перемещение равно нулю ωА= 0.

Формула Гука для определения абсолютной деформации участка

Определяем перемещения:

2016-09-04 12-32-09 Скриншот экрана

Строим эпюру перемещений ω.

2019-10-03_22-47-42

Задача решена.

На стальной стержень действует продольная сила Р и собственный вес (γ = 78 кН/м3). Найти перемещение сечения 1 -1.

Дано: Е =2·105 МПа, А = 11 см2, а = 3,0 м, в = 3,0 м, с= 1,3 м, Р = 2 кН.

Учет собственного веса

Перемещение сечения 1 -1 будет складываться из перемещения от действия силы Р, от действия собственного веса выше сечения и от действия собственного веса ниже сечения. Перемещение от действия силы Р будет равно удлинению участка стержня длиной в+а ,расположенного выше сечения 1 -1. Нагрузка Р вызывает удлинение только участка а, так как только на нем имеется продольная сила от этой нагрузки. Согласно закону Гука удлинение от действия силы Р будет равно: Определим удлинение от собственного веса стержня ниже сечения 1 -1.

Обозначим его как . Оно будет вызываться собственным весом участка с и весом стержня на участке а+в

2015-03-27 19-13-42 Скриншот экрана

Определим удлинение от собственного веса стержня выше сечения 1 -1.

Обозначим его как Оно будет вызываться собственным весом участка а+в

Тогда полное перемещение сечения 1-1:

Т.е, сечение 1-1 опустится на 0,022 мм.

Абсолютно жесткий брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров. Требуется: 1) найти усилия и напряжения в стержнях, выразив их через силу Q; 2) Найти допускаемую нагрузку Qдоп, приравняв большее из напряжений в двух стержнях к допускаемому напряжению ; 3) найти предельную грузоподъемность системы , если предел текучести 4) сравнить обе величины, полученные при расчете по допускаемым напряжениям и предельным нагрузкам. Размеры: а=2,1 м, в=3,0 м, с=1,8 м, площадь поперечного сечения А=20 см2

2015-03-16 22-58-57 Скриншот экрана

Данная система один раз статически неопределима. Для раскрытия статической неопределимости необходимо решить совместно уравнение равновесия и уравнение совместности деформаций стержней.

(1) -уравнение равновесия

Составим деформационную схему — см. рис. Тогда из схемы: (2)

По закону Гука имеем:

Длины стержней: Тогда получим:

2015-03-17 21-00-27 Скриншот экрана Подставим полученное соотношение в уравнение (1):

2015-03-17 21-02-52 Скриншот экрана

Определяем напряжение в стержнях:

2015-03-17 21-03-51 Скриншот экрана

Допускаемая нагрузка:

В предельном состоянии: Подставим полученные соотношения в уравнение (1):

2015-03-17 21-29-14 Скриншот экрана

При сравнении видим увеличение нагрузки:

Колонна, состоящая из стального стержня и медной трубы, сжимается силой Р. Длина колонны ℓ. Выразить усилия и напряжения, возникающие в стальном стержне и медной трубе. 2015-03-16 21-25-06 Скриншот экрана Проведем сечение 1 — 1 и рассмотрим равновесие отсеченной части 2015-03-16 21-26-07 Скриншот экрана

Составим уравнение статики: NC+ NM — P= 0 , NC+ NM = P (1)

Задача статически неопределима. Уравнение совместности деформации запишем из условия, что удлинения стального стержня и медной трубы одинаковы: (2) или Сократим обе части на длину стержня и выразим усилие в медной трубе через усилие в стальном стержне :

(3) Подставим найденное значение в уравнение (1), получим:

2015-03-16 21-52-13 Скриншот экрана

При совместной работе всегда сильнее напряжен элемент из материала с большим модулем упругости. При ЕС = 2·105 МПа, ЕМ = 1·105 МПа:

Для колонны определить напряжения на всех участках. После приложения силы Р зазор закрывается, Р = 200 кН, Е = 2.105 МПа, А = 25 см2 2015-03-14 15-31-51 Скриншот экрана После приложения силы Р возникнут усилия в защемлениях. Обозначим их как C и В.

Составим уравнение статики: ∑y = 0; С + В — Р = 0; (1)

Дополнительное уравнение совместности деформаций: ∆ℓ1+∆ℓ2=0,3 мм (2);

Чтобы найти абсолютную деформацию, необходимо знать продольную силу на участке. На первом участке продольная сила равна С, на втором разности (С- Р). Подставим эти значения в выражения абсолютных деформаций: (3)

Подставляем выражение (3) в выражение (2) и находим: С = 150 кН, а из (1) B = 50 кН .

Тогда напряжения на участках:

2015-03-14 16-39-33 Скриншот экрана

На трех стальных стержнях подвешена жесткая балка; стержень 2 выполнен короче проектного. Определить напряжения в стержнях после сборки системы. Дано:

Схема заданной системы

После завершения сборки в данной системе жесткая балка повернется и займет новое положение.

Схема деформирования

Точки С, D и К переместятся в положения С1, D1 и К1

Согласно картине деформирования СС1=Δℓ1, DD1=Δ−D1D2 = Δ−Δℓ2, KK1= Δℓ3, при этом стержни 1 и 3 испытывают сжатие, а стержень 2 — растяжение.

В соответствии со схемой деформирования уравнение равновесия примет вид: 2015-02-22 18-57-03 Скриншот экрана

Дополнительные уравнения можно получить на основе анализа схемы деформирования; из подобия треугольников ВСС1 и BDD1, треугольников ВСС1 и BKK1следует:

2015-02-22 18-59-07 Скриншот экрана

Согласно закона Гука абсолютные деформации:

Тогда дополнительные уравнения запишутся следующим образом: Решая совместно данную систему полученных дополнительных уравнений и уравнение равновесия , получим:

N1=14,3 кН (стержень сжат), N2=71,5 кН (стержень растянут), N3=42,9 кН (стержень сжат).

Таким образом, искомые напряжения в стержнях имеют значения: 2015-02-22 19-04-53 Скриншот экрана Задача решена.

Ступенчатый медный стержень нагревается от температуры tН=20ºС до tК=50ºС. Проверить прочность стержня. Дано:

2015-02-22 16-30-22 Скриншот экрана 2015-02-22 16-32-06 Скриншот экрана

Составим уравнение равновесия стержня в предположении замены внешних связей реактивными силами: Как видим ,система статически неопределима, и для ее решения требуется дополнительное уравнение.

Уравнение совместности деформаций следует из условия, что перемещения внешних связей равны 0 — WВ=0 или WК=0. Таким образом: 2015-02-22 16-39-23 Скриншот экрана 2015-02-22 16-40-25 Скриншот экрана Откуда:

2015-02-22 16-41-36 Скриншот экрана

В результате RB=20723Н.

Нормальные силы и напряжения на участках: 2015-02-22 16-42-40 Скриншот экрана

Согласно результатам расчетов σmax=│69,1│MПа, при этом σmax< σadm, (69,1<80). Следовательно, условие прочности стержня выполняется.

Расчет стержня с зазором. Для стального ступенчатого стержня при наличии зазора между нижним торцом и опорой требуется: построить эпюры нормальных сил и напряжений, перемещений; проверить прочность. Дано:

Схема стержня; эпюры нормальных сил, напряжений и перемещений

Составим уравнение равновесия стержня:

В нем два неизвестных, система один раз статически неопределима ,требуется дополнительное уравнение — уравнение деформаций.

Дополнительное уравнение можно записать из условия закрытия зазора в процессе деформирования стержня:

Для рассматриваемых участков их абсолютные деформации: 2015-02-21 17-12-34 Скриншот экрана

Определим нормальные (продольные) силы методом сечений, идем от стены к зазору:

Подставим все найденные значения в дополнительное уравнение:

2015-02-21 17-17-48 Скриншот экрана

После подстановки исходных данных и сокращений: 2015-02-21 17-18-51 Скриншот экрана

Из уравнения равновесия получаем:

Таким образом, RВ=40,74 кН, RК=9,26 кН.

Расчет нормальных сил: 2015-02-21 17-21-35 Скриншот экрана Строим эпюру N

Расчет нормальных напряжений: 2015-02-21 17-23-06 Скриншот экрана Строим эпюру нормальных напряжений

Расчет перемещений характерных сечений.

Принимается правило знаков для перемещений: вниз — положительные, вверх — отрицательные. 2015-02-21 17-24-53 Скриншот экрана Строим эпюру перемещений.

Из эпюры нормальных напряжений видно, что:

Следовательно, условие прочности стержня не выполняется.

Навигация по записям

Литература:

Киржанова Е. А., Хуторянский В. В., Балабушевич Н. Г., Харенко А. В., Демина Н. Б. Методы анализа мукоадгезии: от фундаментальных исследований к практическому применению в разработке лекарственных форм. Разработка и регистрация лекарственных средств. 2014; 3(8): 66–80. DOI: 10.33380/2305-2066-2019-8-4-27-31.
А.В. Ланцова, Е.В. Санарова, Н.А. Оборотова и др. Разработка технологии получения инъекционной лекарственной формы на основе отечественной субстанции производной индолокарбазола ЛХС-1208 // Российский биотерапевтический журнал. 2014. Т. 13. № 3. С. 25-32.
https://prosopromat.ru/sopromat/centralnoe-osevoe-rastyazhenie-szhatie-sterzhnej.html.
https://sopromat.in.ua/textbook/axial-tension.
https://prosopromat.ru/category/zadachi/rastyazhenie-szhatie-zadachi.
Patil H., Tiwari R. V., Repka M. A. Recent advancements in mucoadhesive floating drug delivery systems: A mini-review. Journal of Drug Delivery Science and Technology. 2016; 31: 65–71.DOI: 10.1016/j.jddst.2015.12.002.
Patil H., Tiwari R. V., Repka M. A. Recent advancements in mucoadhesive floating drug delivery systems: A mini-review. Journal of Drug Delivery Science and Technology. 2016; 31: 65–71.DOI: 10.1016/j.jddst.2015.12.002.
Moustafine R. I., Bukhovets A. V., Sitenkov A. Y., Kemenova V. A., Rombaut P., Van den Mooter G. Eudragit® E PO as a complementary material for designing oral drug delivery systems with controlled release properties: comparative evaluation of new interpolyelectrolyte complexes with countercharged Eudragit® L 100 copolymers. Molecular Pharmaceutics. 2013; 10(7): 2630–2641. DOI: 10.1021/mp4000635.