Список функций, изученных в 7 и 8 классе
Функция | Формула | График | Раздел справочника |
Прямая пропорциональность | y = kx | Прямая | 7 кл., §37 |
Линейная функция | y = kx+b | Прямая | 7 кл., §38-39 |
Обратная пропорциональность | $ y = frac{k}{x} $ | Гипербола | 8 кл., §6 |
Квадрат числа | $ y=x^2$ | Парабола | 8 кл., §18 |
Квадратный трёхчлен | $ y = ax^2+bc+c$ | Парабола | 8 кл., §28-29 |
Квадратный корень | $ y = sqrt{x}$ | Парабола | 8 кл., §22 |
Растяжение и сжатие графика по оси OX
Сравним графики пар функций, которые в общем виде можно записать так:
$$ y_1 = f(x), y_2 = f(px) $$
где $p gt 1$, произвольный положительный множитель.
Пусть p = 2.
Парабола: $y_1 = f(x) = x^2$ $ y_2 = f(2x) = (2x)^2 = 4x^2 $ $y_2 = y_1 при x_2 = frac{1}{2} x_1$ График сжимается в 2 раза по оси OX |  |
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = f(2x) = frac{4}{(2x)} = frac{2}{x}$ $ y_2 = y_1 при x_2 = frac{1}{2} x_1 $ График сжимается в 2 раза по оси OX |
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = f(2x) = sqrt{2x}$ $y_2=y_1 при x_2 = frac{1}{2} x_1$ График сжимается в 2 раза по оси OX |
|
Теперь сравним пары функций с делением на p:
$$ y_1 = f(x), quad y_2 = f left( frac{x}{p} right), quad p gt 1 $$
Пусть p = 2
Парабола: $y_1 = f(x) = x^2$ $ y_2 = f left(frac{x}{2}right) = left(frac{x}{2}right)^2 = frac{x^2}{4} $ $y_2 = y_1 при x_2 = 2x_1$ График растягивается в 2 раза по оси OX |  |
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = f left(frac{x}{2}right) = frac{4}{x/2} = frac{8}{x}$ $ y_2 = y_1 при x_2 = 2x_1$ График растягивается в 2 раза по оси OX |
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = f left(frac{x}{2}right) = sqrt{frac{x}{2}}$ $y_2=y_1 при x_2 = 2x_1$ График растягивается в 2 раза по оси OX |
|
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = f(px), quad p gt 1 $$
график второй функции сжимается в p раз по оси OX по сравнению с графиком первой функции.
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = f Biggl(frac{x}{p}Biggr), quad p gt 1 $$
график второй функции растягивается в p раз по оси OX по сравнению с графиком первой функции.
Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)
Растяжение и сжатие графика по оси OY
Сравним графики пар функций, которые в общем виде можно записать так:
$$ y_1 = f(x), quad y_2 = Af(x) $$
где $A gt 1$, произвольный положительный множитель.
Пусть A = 2.
Парабола: $y_1 = f(x) = x^2$ $ y_2 = 2f(x) = 2x^2 $ $y_2 = 2y_1 при x_2 = x_1$ График растягивается в 2 раза по оси OY |  |
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = 2f(x) = frac{8}{x}$ $ y_2 = 2y_1 при x_2 = x_1$ График растягивается в 2 раза по оси OY |
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = 2f(x) = 2sqrt{x}$ $y_2 = 2y_1 при x_2 = x_1$ График растягивается в 2 раза по оси OY |
|
Теперь сравним пары функций с делением на A:
$$ y_1 = f(x), quad y_2 = frac{1}{A} f(x), quad A gt 1 $$
Пусть A = 2
Парабола: $y_1 = f(x) = x^2$ $ y_2 = frac{1}{2}f(x) = frac{x^2}{2}$ $y_2 = frac{1}{2}y_1 при x_2 = x_1$ График сжимается в 2 раза по оси OY |  |
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = frac{1}{2}f(x) = frac{2}{x}$ $ y_2 = frac{1}{2}y_1 при x_2 = x_1$ График сжимается в 2 раза по оси OY |
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = frac{1}{2}f(x) = frac{sqrt{x}}{2}$ $y_2 = frac{1}{2}y_1 при x_2 = x_1$ График сжимается в 2 раза по оси OY |
|
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = Af(x), quad A gt 1 $$
график второй функции растягивается в A раз по оси OY по сравнению с графиком первой функции.
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = frac{1}{A} f(x), quad A gt 1 $$
график второй функции сжимается в A раз по оси OY по сравнению с графиком первой функции.
Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)
Примеры
Пример 1. Постройте в одной координатной плоскости графики функций:
$$ y = sqrt{x}, y = sqrt{3x}, y = sqrt{frac{x}{3}}, y = 3sqrt{x} $$
Сделайте выводы.

По сравнению с графиком $y = sqrt{x}$:
- график функции $y = sqrt{3x}$ сжимается в 3 раза по оси OX(←)
- график функции $y = sqrt{frac{x}{3}}$ растягивается в 3 раза по оси OX(→)
- график функции $y = 3sqrt{x}$ растягивается в 3 раза по оси OY(↑)
Пример 2*. Постройте в одной координатной плоскости графики функций:
$$ y = f(x), y = f(2x), y = f Biggl(frac{x}{2}Biggr), y = 2f(x) $$
где $f(x) = x^2+3x+2$
Сделайте выводы.
Исходная функция $y = f(x) = x^2+3x+2$
Остальные функции
$$ y = f(2x) = (2x)^2+3 cdot (2x)+2 = 4x^2+6x+2 $$
$$ y = fBiggl(frac{x}{2}Biggr) = Biggl(frac{x}{2}Biggr)^2+3 cdot Biggl(frac{x}{2}Biggr) +2 = frac{x^2}{4}+ frac{3}{2} x+2 $$
$$ y = 2f(x) = 2x^2+6x+4 $$
Получаем:

По сравнению с графиком $y = f(x) = x^2+3x+2$:
- график функции y = f(2x) сжимается в 2 раза по оси OX(→)
- график функции $y = f left(frac{x}{2}right)$ растягивается в 2 раза по оси OX(←)
- график функции y = 2f(x) растягивается в 2 раза по оси OY(↑)
Рейтинг пользователей
Преобразования графиков тригонометрических функций
Общие принципы преобразования графиков функций изучались нами в главе 8, (см. §47, §48, §50 справочника для 8 класса). В этом параграфе мы рассмотрим особенности тригонометрических функций при использовании этих преобразований.
п.1. Растяжение и сжатие графиков тригонометрических функций по оси OX
Общие принципы растяжения и сжатия графиков по оси OX:
При сравнении графиков двух функций $$ y_1=f(x), y_2=f(px), pgt 1 $$ график второй функции сжимается в p раз по оси OX по сравнению с графиком первой функции.
При сравнении графиков двух функций $$ y_1=f(x), y_2=f(frac{x}{p}), pgt 1 $$ график второй функции растягивается в p раз по оси OX по сравнению с графиком первой функции.
Эти принципы справедливы и для тригонометрических функций.
Тригонометрические функции являются периодическими: синус и косинус с периодом 2π, тангенс и котангенс — с периодом π. Получаем следствие общих принципов:
При сравнении двух тригонометрических функций $$ y_1=f(x), y_2=f(px), pgt 1 $$ период второй функции уменьшается в p раз: $$ T_2=frac{T_1}{p} $$
При сравнении двух тригонометрических функций $$ y_1=f(x), y_2=f(frac{x}{p}), pgt 1 $$ период второй функции увеличивается в p раз: $$ T_2=pT_1 $$
Например:
Построим в одной системе координат три графика: $$ f(x)=sinx, g(x)=sin2x, h(x)=sinfrac{x}{2} $$ 
Период колебаний функции (g(x)=sin2x) в 2 раза меньше: (T_g=frac{2pi}{2}=pi).
Период колебаний функции (h(x)=sinfrac{x}{2}) в 2 раза больше: (T_h=2cdot 2pi=4pi).
п.2. Растяжение и сжатие графиков тригонометрических функций по оси OY
Общие принципы растяжения и сжатия графиков по оси OY:
При сравнении графиков двух функций $$ y_1=f(x), y_2=Af(x), Agt 1 $$ график второй функции растягивается в A раз по оси OY по сравнению с графиком первой функции.
Общий принцип сжатия графиков:
При сравнении графиков двух функций $$ y_1=f(x), y_2=frac{1}{A}f(x), Agt 1 $$ график второй функции сжимается в A раз по оси OY по сравнению с графиком первой функции.
Эти принципы справедливы и для тригонометрических функций.
Т.к. для графиков синуса и косинуса (синусоиды) характерна амплитуда колебаний, то также говорят, что:
- умножение на параметр (Agt 1) увеличивает амплитуду колебаний в (A) раз;
- деление на параметр (Agt 1) уменьшает амплитуду колебаний в (A) раз.
Например:
1) Построим в одной системе координат три графика: $$ f(x)=cosx, g(x)=2cosx, h(x)=frac{1}{2}cosx $$ 
Умножение на (A=2) увеличивает амплитуду колебаний в 2 раза.
Область значений функции (g(x)=2cosx: yin[-2;2]). График растягивается по оси OY.
Деление на (A=2) уменьшает амплитуду колебаний в 2 раза. Область значений функции (h(x)=frac12 cosx: yinleft[-frac12; frac12right]). График сжимается по оси OY.
2) Теперь построим $$ f(x)=tgx, g(x)=2tgx, h(x)=frac{1}{2}tgx $$ 
В этом случае хорошей иллюстрацией растяжения по оси OY при умножении и сжатия по оси OY при делении на (A=2) служит поведение функции при (x=fracpi4). $$ fleft(fracpi4right)=tgleft(fracpi4right)=1, gleft(fracpi4right)=2tgleft(fracpi4right)=2, hleft(fracpi4right)=frac12 tgleft(fracpi4right)=frac12 $$ Аналогично — для любого другого значения аргумента x.
п.3. Параллельный перенос графиков тригонометрических функций по оси OX
Общие принципы переноса по оси OX:
При сравнении графиков двух функций $$ y_1=f(x), y_2=f(x+a), agt 0 $$ график второй функции смещается влево на a по оси OX по сравнению с графиком первой функции.
При сравнении графиков двух функций $$ y_1=f(x), y_2=f(x-a), agt 0 $$ график второй функции смещается вправо на a по оси OX по сравнению с графиком первой функции.
Эти принципы справедливы и для тригонометрических функций.
При этом параметр x называют начальной фазой колебаний.
При сравнении двух тригонометрических функций (y_1=f(x)) и (y_2=f(xpm a)) говорят, что у второй функции сдвиг по фазе равен (pm a).
Например:
1) Построим в одной системе координат три графика: $$ f(x)=sinx, g(x)=sinleft(x+fracpi4right), h(x)=sinleft(x-fracpi4right) $$ 
Функция (g(x)=sinleft(x+fracpi4right)) сдвинута на (fracpi4) влево по сравнению с (f(x))
Функция (h(x)=sinleft(x-fracpi4right)) сдвинута на (fracpi4) вправо по сравнению с (f(x))
п.4. Параллельный перенос графиков тригонометрических функций по оси OY
Общие принципы переноса по оси OY:
При сравнении графиков двух функций $$ y_1=f(x), y_2=f(x)+a, agt 0 $$ график второй функции смещается вверх на a по оси OY по сравнению с графиком первой функции.
При сравнении графиков двух функций $$ y_1=f(x), y_2=f(x)-a, agt 0 $$ график второй функции смещается вниз на a по оси OY по сравнению с графиком первой функции.
Эти принципы справедливы и для тригонометрических функций.
Например:
1) Построим в одной системе координат три графика: $$ f(x)=sinx, g(x)=sinx+1, h(x)=sinx-1 $$ 
Функция (g(x)=sinx+1) сдвинута на 1 вверх по сравнению c (f(x))
Функция (h(x)=sinx-1) сдвинута на 1 вниз по сравнению с (f(x))
п.5. Общее уравнение синусоиды
Синусоида — плоская кривая, которая задается в прямоугольной системе координат уравнением: $$ y(x)=Asin(cx+d)+B $$ где
A — амплитуда, характеризует растяжение графика по оси OY
B — вертикальный сдвиг, характеризует сдвиг графика по оси OY (вверх/вниз)
c — циклическая частота, характеризует период колебаний и растяжение графика по оси OX
d- начальная фаза, характеризует сдвиг графика по оси OX(влево/вправо)
График (y(x)=Acos(cx+d)+B) также называют синусоидой. Термин «косинусоида» употребляется относительно редко.
Поскольку график косинуса получается из графика синуса сдвигом по фазе на π/2 влево, вводить термин «косинусоида» излишне.
Например:
Построим график (g(x)=3sinleft(2x+fracpi2right)-1)
По сравнению с (f(x)=sinx):
- (A=3) — график растянут по оси OY в 3 раза
- (c=2) — период меньше в 2 раза T=π, график сжат в 2 раза по оси OX
- (d=fracpi2) — начальная фаза положительная, график сдвинут на (frac{pi}{2cdot 2}=fracpi4) влево
- (B=-1) — график сдвинут по оси OY на 1 вниз

п.6. Общее уравнение тангенцоиды
Tангенцоидa — плоская кривая, которая задается в прямоугольной системе координат уравнением: $$ y(x)=Atg(cx+d)+B $$ где
A — амплитуда, характеризует растяжение графика по оси OY
B — вертикальный сдвиг, характеризует сдвиг графика по оси OY (вверх/вниз)
c — циклическая частота, характеризует период колебаний и растяжение графика по оси OX
d- начальная фаза, характеризует сдвиг графика по оси OX(влево/вправо)
График (y(x)=Actg(cx+d)+B) также называют тангенцоидой.
Например:
Построим график (g(x)=frac12 tgleft(frac{x}{2}-fracpi3right)+1)
По сравнению с (f(x)=tgx):
- (A=frac12) — график сжат по оси OY в 2 раза
- (c=frac12) — период больше в 2 раза T=2π, расстояние между асимптотами 2π, график растянут в 2 раза по оси OX
- (d=-fracpi3) — начальная фаза отрицательная, график сдвинут на (frac{pi}{3cdot 1/2}=frac{2pi}{4}) вправо
- (B=1) — график сдвинут по оси OY на 1 вверх

п.7. Примеры
Пример 1.Постройте в одной системе координат графики: $$ f(x)=sinx, g(x)=-sinx, h(x)=cosx $$ Найдите сдвиг по фазе для (g(x)) и (h(x)) в сравнении с (f(x)).

Сдвиг по фазе удобно определять по главной арке синусоиды.
Для (f(x)=sinx) главная арка определена на отрезке (0leq xleq pi)
Для (g(x)=-sinx) главная арка определена на отрезке (-pileq xleq 0), т.е. сдвинута на π влево от (f(x)). Это означает, что: $$ f(x)=g(x+pi), sinx=-sin(x+pi) $$ Для (h(x)=cosx) главная арка определена на отрезке (-fracpi2leq xleq fracpi2), т.е. сдвинута на (fracpi2) влево от (f(x)). Это означает, что: $$ f(x)=hleft(x+fracpi2right), sinx=cosleft(x+fracpi2right) $$
Пример 2. Найдите наименьшие положительные периоды функций:
a) (y=sin5x)
Период синуса (2pi) уменьшается в 5 раз. Получаем: (T=frac{2pi}{5})
б) (y=cospi x)
Период косинуса (2pi) уменьшается в (pi) раз. Получаем: (T=frac{2pi}{pi}=2)
в) (y=tgfrac{x}{4})
Период тангенса (pi) увеличивается в 4 раза. Получаем: (T=4pi)
г) (y=tgleft(2x+frac{pi}{3}right))
Период тангенса (pi) уменьшается в 2 раза. Получаем: (T=fracpi2)
Пример 3. Используя правила преобразования графиков функций, постройте график $$ f(x)=2ctgleft(3x+fracpi6right) $$ По сравнению с (g(x)=tgx):
- (A=2) — график растянут по оси OY в 2 раза
- (c=3) — период меньше в 3 раза (T=fracpi3), расстояние между асимптотами (fracpi3), график сжат в 3 раза по оси OX
- (d=-fracpi6) — начальная фаза положительная, график сдвинут на (frac{pi}{6cdot 3}=frac{pi}{18}) влево
Расположение нулей: $$ tgleft(3x+fracpi6right)=0Rightarrow 3x+fracpi6=pi kRightarrow 3x=-fracpi6+pi kRightarrow x =-frac{pi}{18}+frac{pi k}{3} $$ Вертикального сдвига нет, нули расположены на оси OX.
Расположение асимптот: $$ 3x+fracpi6nefracpi2+pi kRightarrow 3xnefracpi3+pi kRightarrow xnefracpi9+frac{pi k}{3} $$ Пересечение главной ветви с осью OY: (x=0, y=2tgfracpi6=frac{2}{sqrt{3}})
С учетом периода (fracpi3) получаем семейство дополнительных точек для построения графика (left(frac{pi k}{3}; frac{2}{sqrt{3}}right)).

Пример 4. Определите графически, сколько корней имеет уравнение на отрезке: a) (sinx=sin2x) при (0leq xleq 3pi)

Ответ: 7 корней
б) (cosfrac{x}{2}=cos2x) при (-2pileq xleq 2pi)

Ответ: 7 корней
3. Деформация (сжатие и растяжение)
3.1 Сжатие (растяжение) графика вдоль оси ординат
Рассмотрим функцию вида y=A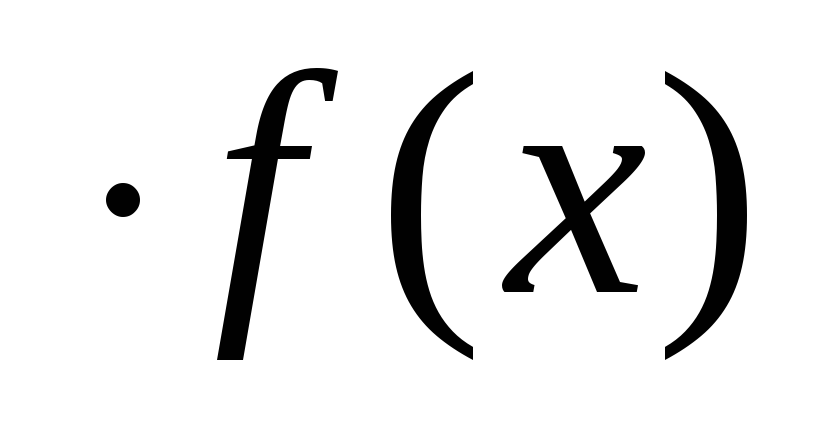 , где A>0. Нетрудно заметить, что при равных значениях аргумента ординаты графика этой функции будут в A раз больше ординат графика функции y=f(x) при A>1 или в
, где A>0. Нетрудно заметить, что при равных значениях аргумента ординаты графика этой функции будут в A раз больше ординат графика функции y=f(x) при A>1 или в 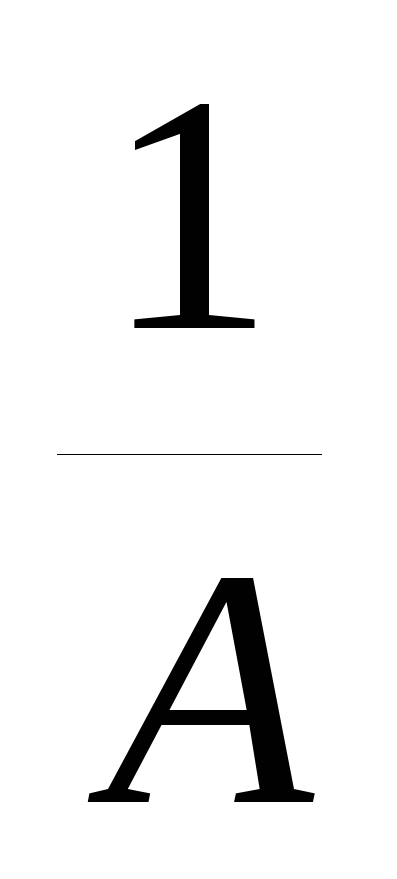 раз меньше ординат графика функцииy=f(x) при A<1. Таким образом, получаем следующее правило.
раз меньше ординат графика функцииy=f(x) при A<1. Таким образом, получаем следующее правило.
Для построения графика функции y=A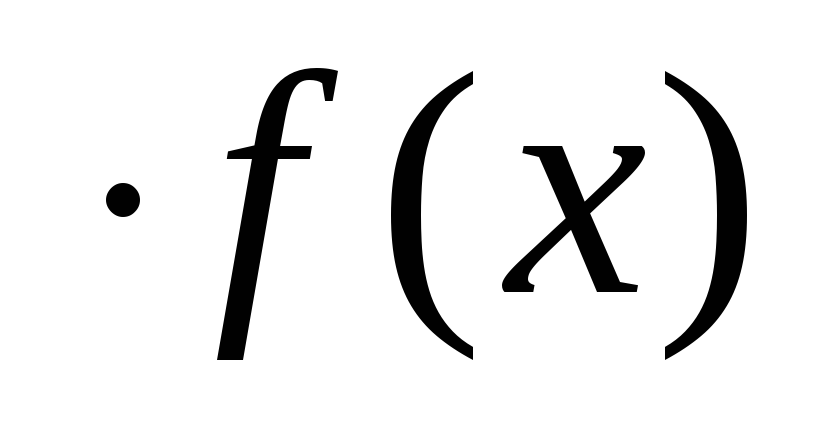 следует построить график функции y=f(x) и увеличить его ординаты в A раз при A>1 (произвести растяжение графика вдоль оси ординат) или уменьшить его ординаты в
следует построить график функции y=f(x) и увеличить его ординаты в A раз при A>1 (произвести растяжение графика вдоль оси ординат) или уменьшить его ординаты в 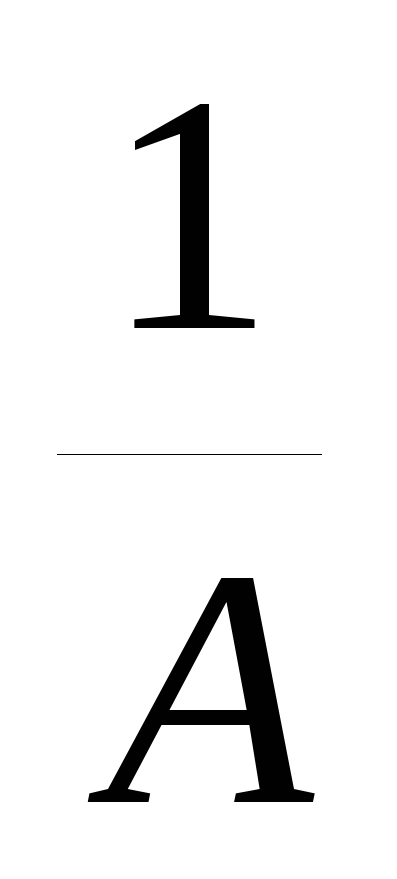 раз приA<1 (произвести сжатие графика вдоль оси ординат). Полученный график является графиком функции y=A
раз приA<1 (произвести сжатие графика вдоль оси ординат). Полученный график является графиком функции y=A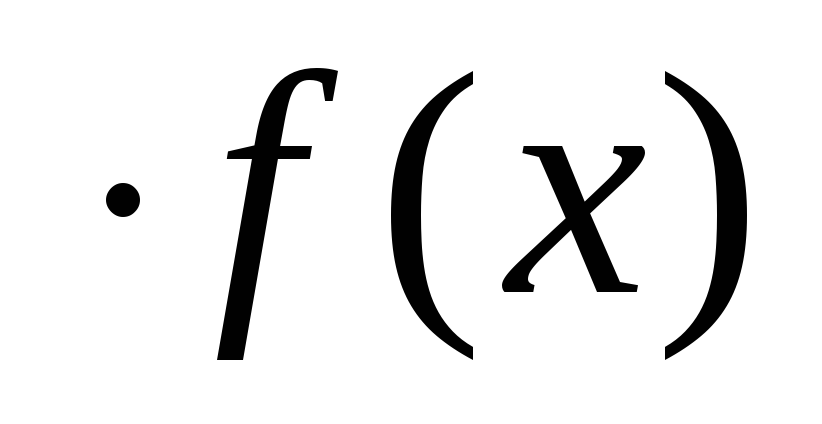 .
.
Пример 13. Построить график функции y=2cos x.
Р е ш е н и е: Строим график функции y=cos x (рис.16 — пунктирная кривая) и растяжением этого графика вдоль оси ординат в 2 раза получаем график функции y=2cos x (сплошная кривая).
Пример 14. Построить график функции y=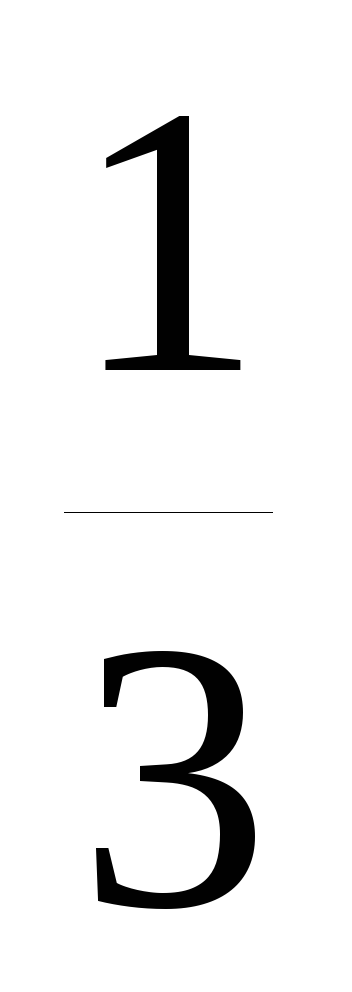 x2.
x2.
Р е ш е н и е: Строим график функции y=x2 и сжатием этого графика в 3 раза вдоль оси ординат получаем график функции y=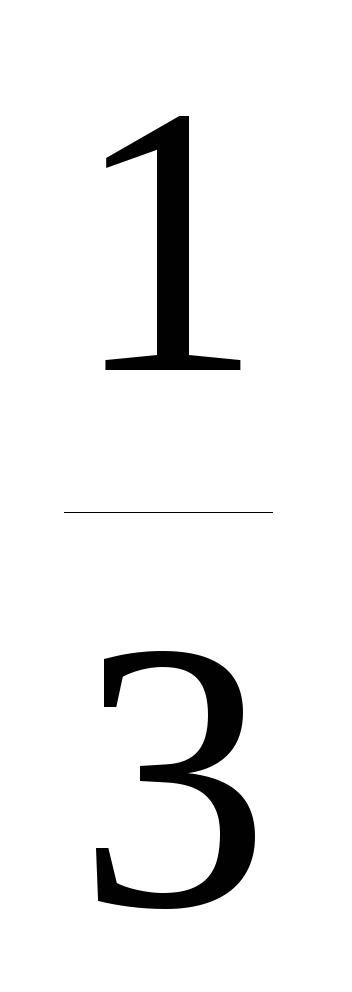 x2 (рис.17).
x2 (рис.17).
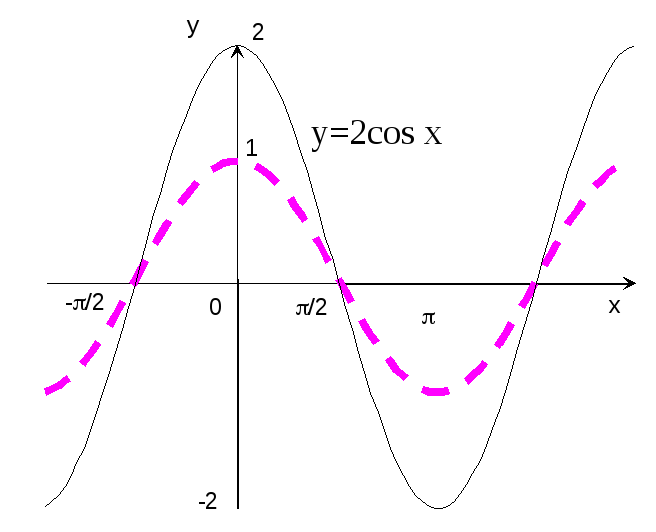
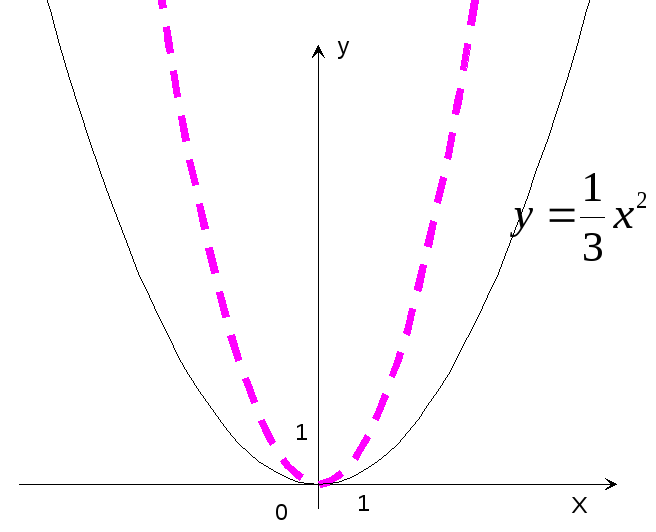
Рис.16
Рис.17
3.2. Сжатие (растяжение) графика вдоль оси абсцисс
Пусть требуется построить график функции y=f(x), где >0. Рассмотрим функцию y=f(x), которая в произвольной точке x=x1 принимает значение y1=f(x1).
Очевидно, что функция y=f(x) принимает такое же значение в точке x=x2, координата
к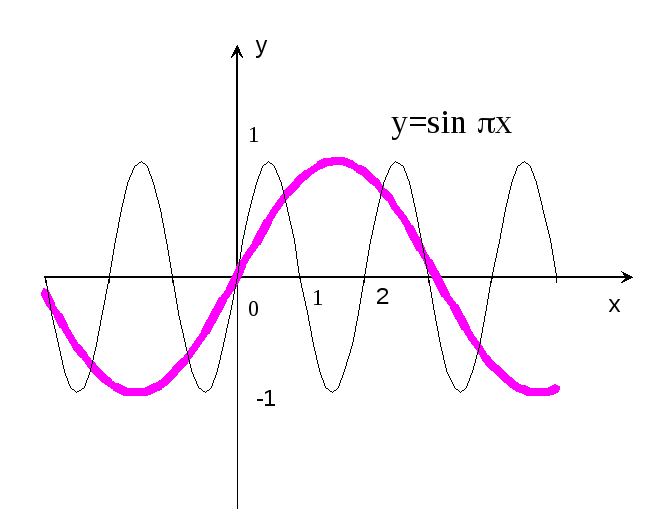 оторой определяется равенствомx1=x2, или x2=
оторой определяется равенствомx1=x2, или x2=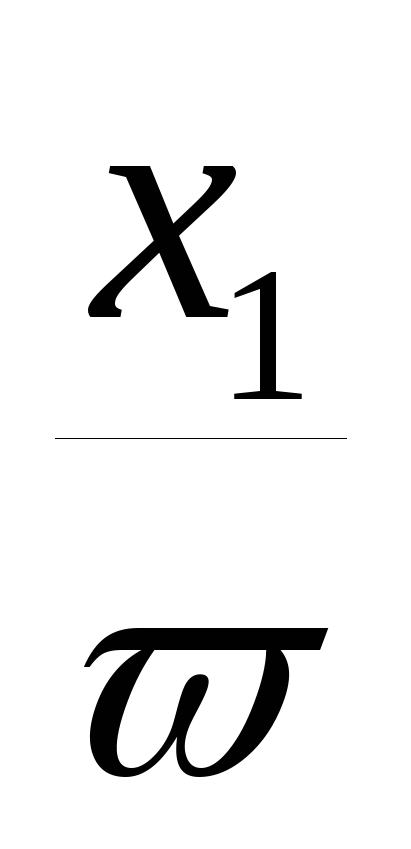 , причём это равенство справедливо для совокупности всех значений x из области определения функции. Следовательно, график функции y=f(x) оказывается сжатым (при >1) или растянутым (при <1) вдоль оси абсцисс относительно графика функции y=f(x). Таким образом, получаем следующее правило.
, причём это равенство справедливо для совокупности всех значений x из области определения функции. Следовательно, график функции y=f(x) оказывается сжатым (при >1) или растянутым (при <1) вдоль оси абсцисс относительно графика функции y=f(x). Таким образом, получаем следующее правило.
Для построения графика функции y=f(x) следует построить график функции y=f(x) и уменьшить его абсциссы в раз при >1 (произвести сжатие графика вдоль оси абсцисс) или увеличить его абсциссы в  раз при<1 (произвести растяжение графика вдоль оси абсцисс). Полученный график является графиком функции y=f(x).
раз при<1 (произвести растяжение графика вдоль оси абсцисс). Полученный график является графиком функции y=f(x).
П
Рис. 18
ример 15.Построить график функции 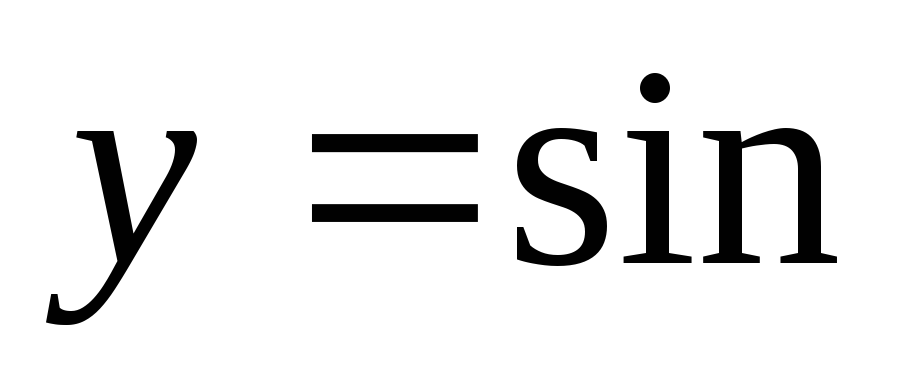 x.
x.
Р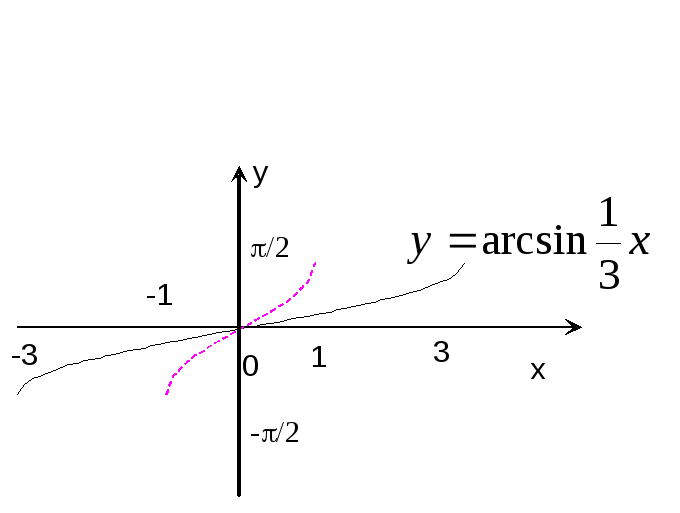 е ш е н и е: Строим график функции
е ш е н и е: Строим график функции 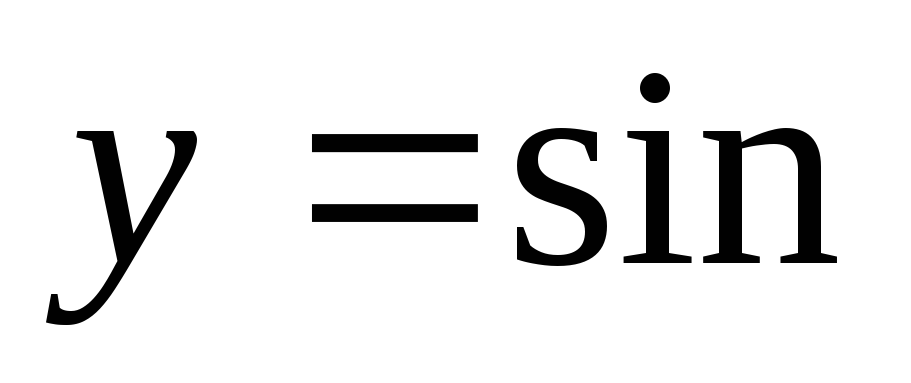 x (рис.18 — пунктирная кривая), и проводя его сжатие в раз вдоль оси абсцисс, получаем график функции
x (рис.18 — пунктирная кривая), и проводя его сжатие в раз вдоль оси абсцисс, получаем график функции 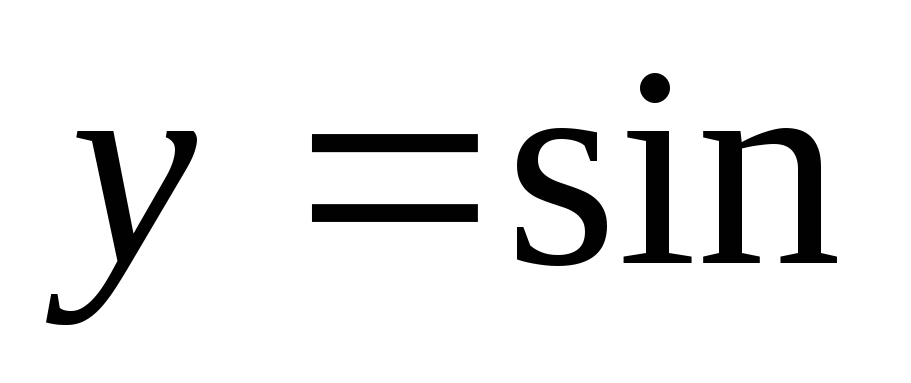 x (сплошная кривая). Период этой функции уже равен не 2, а
x (сплошная кривая). Период этой функции уже равен не 2, а 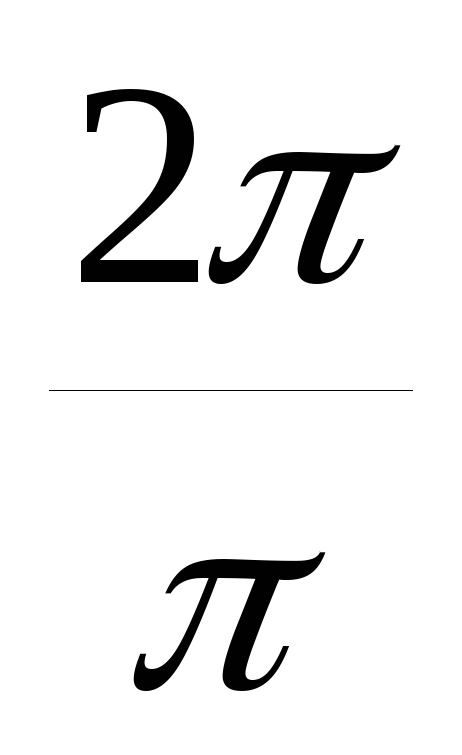 =2. График пересекает ось абсцисс в точкахx=0,
=2. График пересекает ось абсцисс в точкахx=0,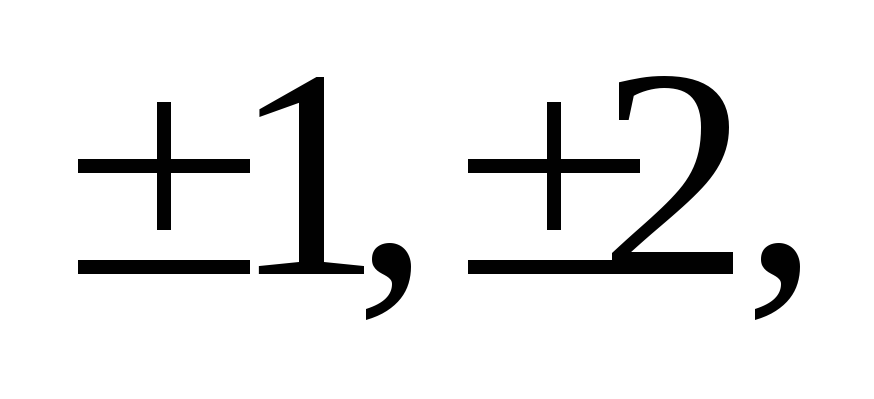 … .
… .
Пример 16. Построить график функции  .
.
Р е ш е н и е: Строим график функции  и, растянув его вдоль оси абсцисс в 3 раза, получаем график функции
и, растянув его вдоль оси абсцисс в 3 раза, получаем график функции .
.
4. Комбинация переноса, отражения и деформации
Рис. 19
Очень часто при построении графиков функций применяют композицию приёмов, изложенных в пунктах 1-3. Последовательное применение ряда таких приёмов позволяет существенно упростить построение графика исходной функции и нередко свести его в конце концов к построению одной из простейших элементарных функций.
Рассмотрим, как с учётом изложенного следует, например, построить график функции вида y=Af(x+a)+b. Запишем исходную функцию в виде y=Af [ ( x+ ) ] +b и схему поэтапного её упрощения (последовательность преобразований):
) ] +b и схему поэтапного её упрощения (последовательность преобразований):
1.y=Af [ ( x+ ) ] + b ; перенос оси абсцисс на b единиц;
) ] + b ; перенос оси абсцисс на b единиц;
2.y=Af [ ( x+ ) ]; перенос оси ординат на
) ]; перенос оси ординат на  единиц;
единиц;
3. y=Af [ x ]; отражение графика относительно оси абсцисс
(этап выполняется только приA<0);
4.y=A· f (x); сжатие или растяжение графика
вдоль оси ординат;
5. y=f (x) отражение графика относительно оси ординат
(этап выполняется только при<0);
6.y=f ( x); сжатие или растяжение вдоль оси абсцисс;
7. y=f ( x);
Проводя построение графика шаг за шагом в порядке, обратном порядку упрощения вида функции с учётом всех указанных правил, получим график исходной функции.
Пример 17. Построить график функции y=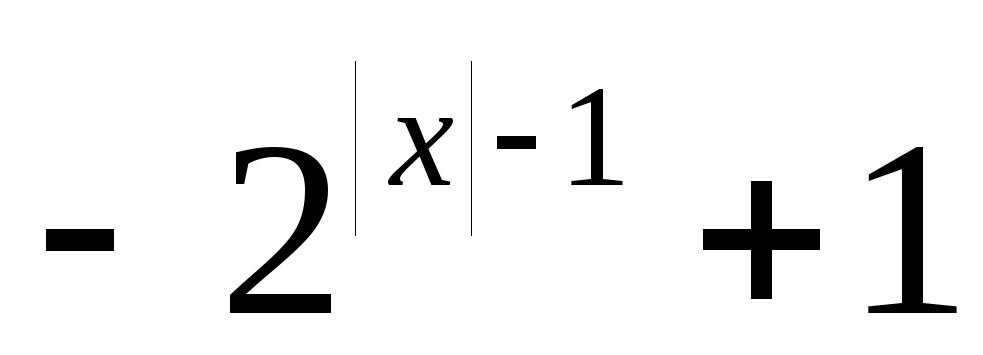 .
.
Ре ш е н и е: Схема построения графика :
y=
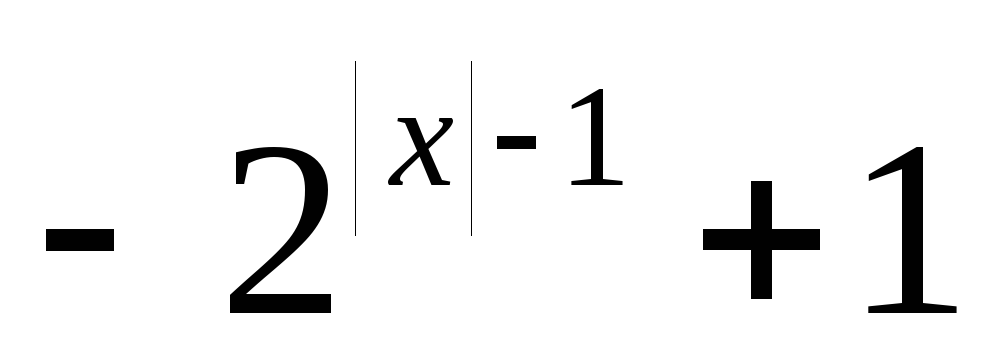
x
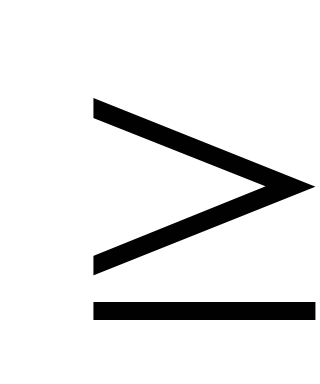 0, y=
0, y=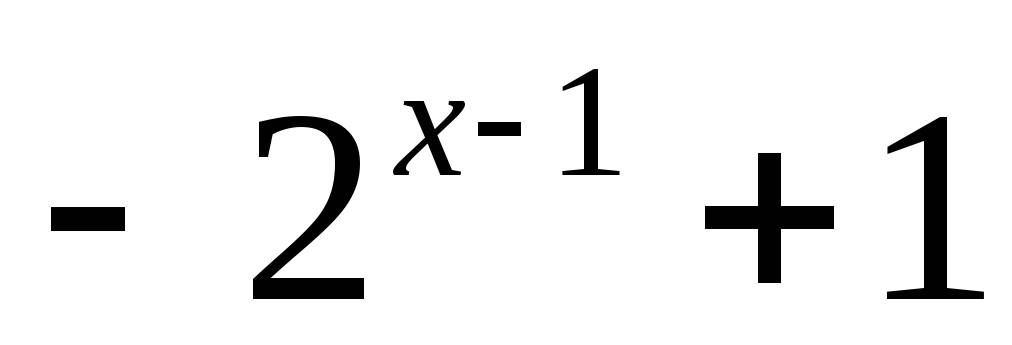 ;
;y=
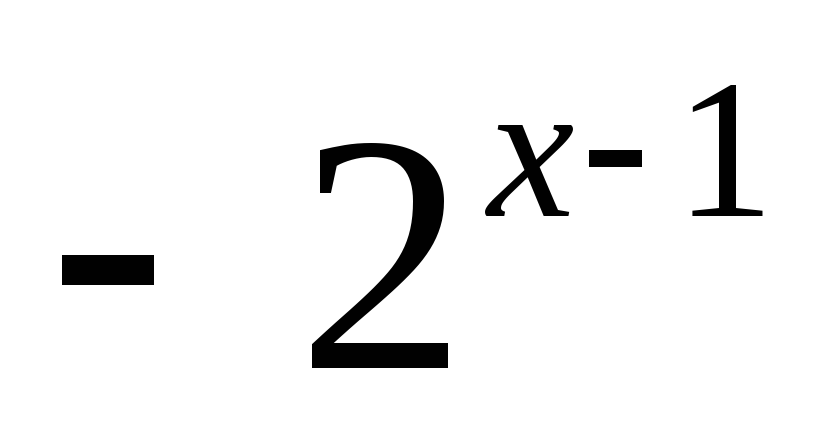 ;
;у=
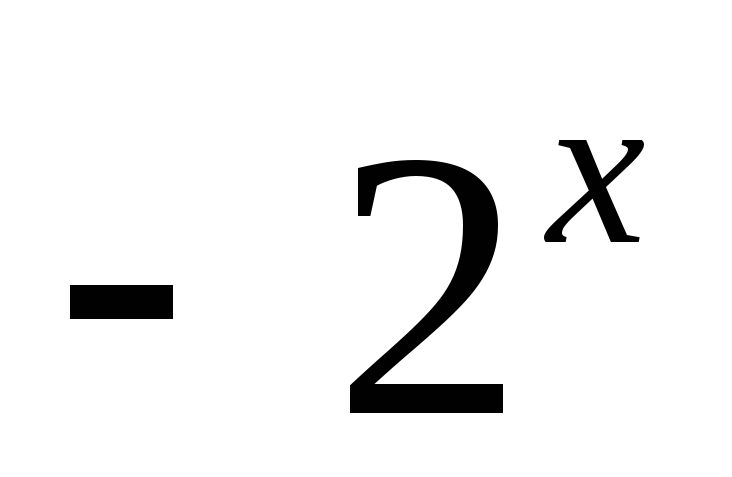 ;
;y=
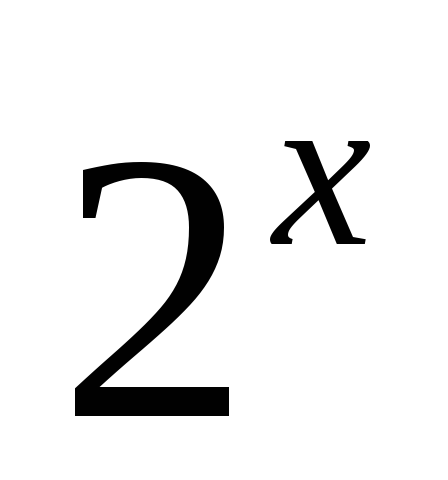 ;
;
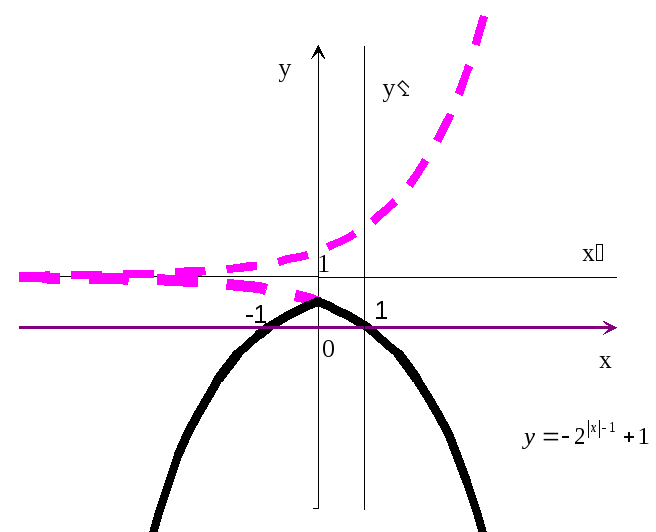
Итак, построение графика исходной функции следует начинать с построения графика функции y=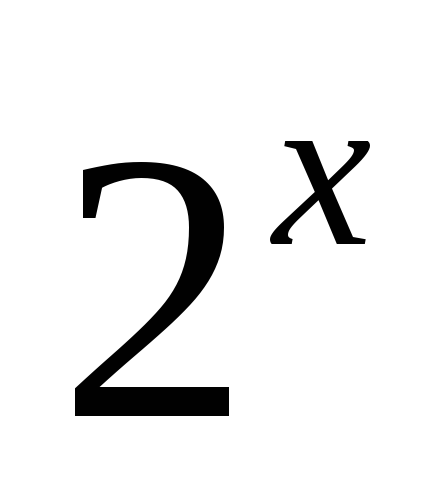 . График (рис.20) пересекает ось ординат в точке
. График (рис.20) пересекает ось ординат в точке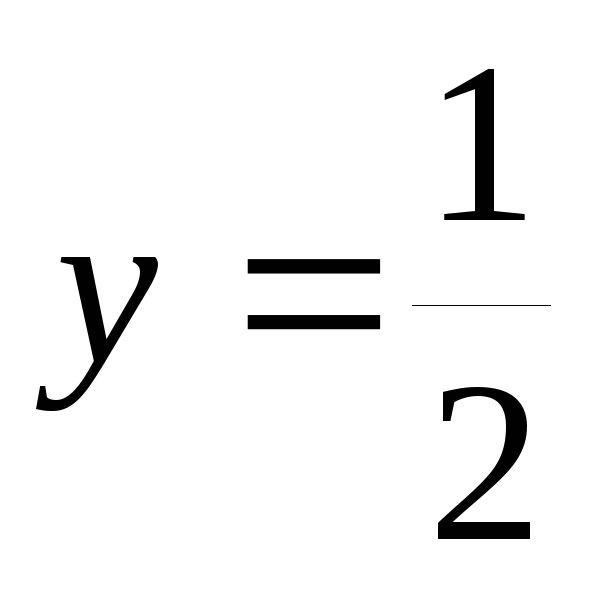 (из условияx=0), а ось абсцисс в точках x=1 (из условия y=0, т.е.
(из условияx=0), а ось абсцисс в точках x=1 (из условия y=0, т.е.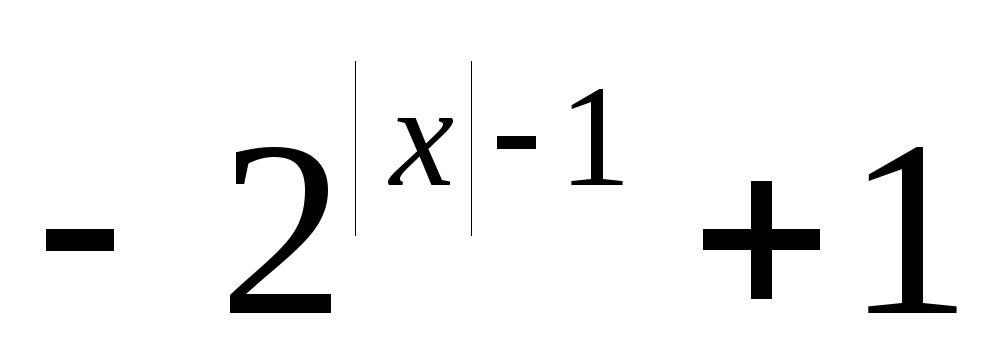 =0).
=0).
 В заключении отметим, что порядок упрощения целесообразно проводить в следующей последовательности.
В заключении отметим, что порядок упрощения целесообразно проводить в следующей последовательности.
Использование чётности или нечётности функции.
Перенос осей.
Отражение и деформация.
Построение же графика, как обычно, выполняется в обратной последовательности.
Рис.20
Задание для самостоятельного выполнения
Ниже приводятся тексты заданий для самостоятельного выполнения. Вам необходимо построить графики функций, оформить работу отдельно от решений по другим предметам и выслать в адрес Хабаровской краевой заочной физико-математической школы.
М.11.2.1 С помощью элементарных преобразований постройте графики следующих функций:
y=x2-2;
y=(x+1)2;
y=sin
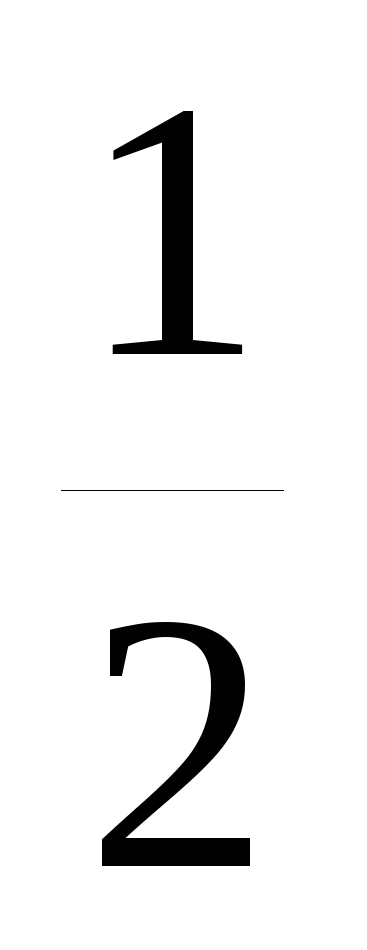 x;
x;y=- 3sin x;
y=tg
 ;
;
М.11.2.2. Написать последовательность преобразований и построить графики следующих функций:
y=
 ;
;y=(x-1)3+2;
y=ln (1-x);
y=tg(-
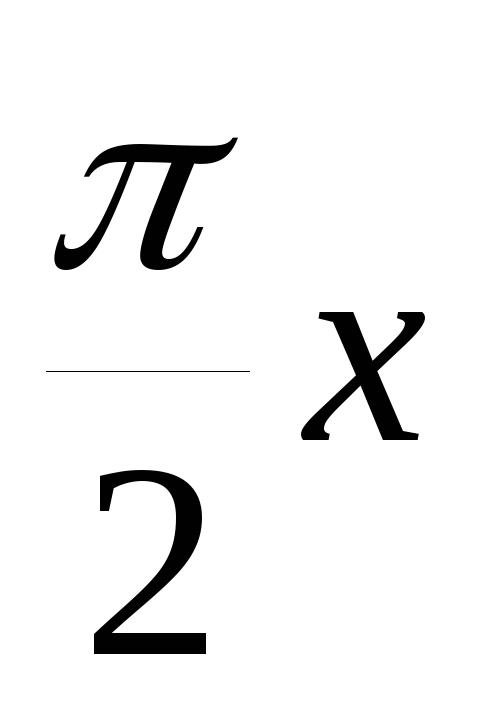 );
);y=
 cos(2x-1)-2.
cos(2x-1)-2.
Хабаровская краевая заочная физико-математическая школа
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|õ¾6¯œÝèK0ä¢X_€’* ¨ÆÖjÔL]G£!¼Ïñs¡¦kð§ D Q)¿5@»IDy*ÜÄ:ü²93’fì£)Ð’-Ò’ O9°¹½ˆdR8àJÏTß èÁF¸¢%ès«d…UwHs[fq]ŒçH2(ŠM¡&˜s?¢à4çörh}‰5R¹ë°×1 ½…Ÿa€GÍé˜à¸$š´©e½?H$hÃGþÙvV©Ýf VG%¨6ßî¹Pµ;êšUª²Lƒ»\Ò¶!·Lá¥^ ïÏ3,%±¾ÿû˧ÚM²W¿yùôa8¼ûtüÃ÷wœ¦-Z¹ÇÔJäŒÏ?Èß~{i‡-;ïðéN…¿-Ÿ~€ßêð7øþ/øÆ?Þq{ø|~ü)¦m°Ë;-Y«ûøEHt ÙÑÌ}ì¾D®ÿŠ~xûÏÅdo1ðd;[ì-[«T‡’fʶtþ[Õÿø{ôüŸ-âºGùQé/Ôm/÷(-GÖ’j¾¼}>|þ÷ê~G/Š) ¤ma˜7ra RÝ·M¡ FÔvî·XÞ§ÎèJ#Ô÷Ý ç¶ø]¿V^lf7{e,¤¬dgV8º˜? gTèê˜ÅiÕhô «ø¨jù@ó»†2°D Â’ χã¾M»&ƒÉLï2þaªnš¸sH6)b²?¦RtÑU,:¤*cZ)ÝcŠ²uŸÞö¥ñéuÚeO|Aë’1¥^µ1Y…*¿qx_o»ÅLzl¥LÍÐ¥È7µÊ™îlÕ¼ìRP°©e8Z é§þš›Ù¼¯HS#Ù:k÷Ë·çøÓT,¸Jÿ»Êd·êX-*Òd¦}óÔp»nRYväenÚŠÐ «:Lé6™ŽR0LÏTŽ Ý´åV¯ÃϺ±PÛ™]þŽÃA訦’xèCK8 …D߃ü2*›uñY>ý¨)»b¾P÷õl ÊK˜T{ø{ˆÖ,ãqÜ)Trø ±)ÁŠ§).2″òsämä+YyŽsƒ7†A-Dª¸’GèÔˆã’`êk×@w~CÎ@ ðeÏŽÆ8Þ¨vùÎã˜z8€ ‘t¨˜4À L¨Q¬ô¿BlײÀŽ2P?i¤DIuA¹‰’¡¡š»üs2uö©¸Û›ìSâëiNó%-Ijø¤’ÐKJ4?´ïs$Oa°ô ¶4_ù»lMjÓ[qËBùFÚÕÔüÐëj¨U¤âAŸP±99H¨´Üšýͼ ìï’»¥ ö¿Ê›Ý»W8}9!ü|xsX%ºhZ-D}£ ÑNIOhn‡Q1¹at8Â*O»¡»~s·j%É6™-Ð|›vX¿} @/õæ.4S¿øs§± «ñMq¤é QѺ¢‡3ÃBÅ™YÙômã@ïx2å*) Ò0ƒ1ù²æYRÍisD ¥í¡¢‡Ò›Ð1FÇ¡ ¢7%àŒÒÎW)-N³ÝMFP®OîBiÈ 8*zä©ü$»§Œ»©Œ=N$¡3v©»ð·»ù»ÖØQnuOŽˆÎ³ãÅtDÕ-OK³˜í°ÊCïJͲwÛ;0 }øN´»½hÇhå]ƒvÆU¨§ÛžnDkgzû ôÕ÷n 2r1XÍ!Rt»-5ýoGdÉ>»êÛ°©b=›BªdŨX)™•T©øn«j1Z?³ªî[•^» ±`qv^N×ëMˆ¹Ñó ë©=€-Ö;Å’xqcÊ.B NDô䈻ò ,6?í$œ± «R£•;DökŸh€ÂX»xêªäìÞ€®c{‘» Ö%™/…nG[zòÊgÀn Æmµ˜õ¶3°»[‰^ST6j2-K ‘»Ælà'»Ïñ(£Ü³·½j’ì‹ }Ï/ùr’ ¶TÚo]·i.d¤cÿ¹’ÂM»Bòk &`Md ×f»Ù©|ÛÓ~Á)÷:n¸u£³;óŽêm gè@Ä@çÿ‰õ½*Áí ýWë»õ+µÝA îÝY·ÒB¯ƒ’¿·ƒR+GÈܬIÏ´ÎM¯ð 7ÄÝìpf$!’ïgÆw˜4bŽÜ™15»®šÐ¦¹ÝÜèœ|ÿq{ƒ½þ§Û]kí¡i&Úùã7Ã’XÏNpÙ6%38l↷°î«o?¾|x’ìpþqø]oMQ×Îá]p¤…è‹Wá.Ã’ŸÒó»Þÿ %œ¥¡ endstream endobj 5 0 obj > endobj 6 0 obj [ 7 0 R] endobj 7 0 obj > endobj 8 0 obj > endobj 9 0 obj > endobj 10 0 obj > endobj 11 0 obj > endobj 12 0 obj > endobj 13 0 obj [ 14 0 R] endobj 14 0 obj > endobj 15 0 obj > endobj 16 0 obj > endobj 17 0 obj > endobj 18 0 obj [ 19 0 R] endobj 19 0 obj > endobj 20 0 obj > endobj 21 0 obj > endobj 22 0 obj > endobj 23 0 obj > endobj 24 0 obj >/F 4/A>/StructParent 10>> endobj 25 0 obj > endobj 26 0 obj > endobj 27 0 obj > stream xœc` øøñ#’*çÍ›W__&¸k×®bl $$Hcì¿ÿìíí9BÐLUUÕåË-4pÒ¤I7n$ÒSt ðJ+ê endstream endobj 28 0 obj > stream xœc` þ£òþC)@•üKU!a œnå endstream endobj 29 0 obj > stream xœì ¯³Êr®;àpE@Ä%HˆAè ÃEüÿ¥«›lc3¬~öÖ·&€_ª««ª««ŠB¡P( …B¡P( …B¡P( …B¡P( …B¡P( …B¡P(«k îè¡Ü ³Ñ:ú@(w»‘Æ.dü}ž)þ]’U•fðM Ið·Uîyð}žåQ¿MÒúȃÉ#(«B‡€ìJ ø’‹uªXP‹Jåͪ* ^ª*GHÃÒ»!£¨rNªµ¤!·J’|»sá’ÐC(©êá© +HE ¿)ˆVù‰ð0áyµ®ÒñÓj°(]¢+ärÁæ«ŠJ+Ë%Å *+ !5ã’&DNR* 9µÅztðiPN††Dò/ƒeÃæ`~*¤†ððfƒ®°)C’Ýøö¾‰Ôª’±=cðO¼jãÇðéÑç@9)« [ kûO «ÿR»¤@ø!aë»DDZâPÀv[0 ÿ]´ðț؈}»Óá «§y ƒå» .* $`ÙXdxäöXë urMª»xès*ð¼°³ñxð, ïèó œlˆbâ¼ÇÄmgÀ‰•’Àϯ܃aOñ»üûúoØõ’‹4†Ýö£Ïƒr.FÂÿz¬` IX:þÏ26c1c`Å9ƒÇÇ‹µÀËWñÀ˜b]ay!Ñ«X&ÁºRŽ>ʹ(S˜ÕAü¬Så…ä·Yžƒ3žU^â/äw)|+#¹JìúÇØdb¸LÁ’=£P¶ã`|œGÁ…r’Ê£€B¡P( …B¡P( …B¡P( …B¡P( …B¡P( …B¡P( …B¡P( …B¡P( …B¡P( …B¡P(ûQˆaYF4,Ó²xü-Ë»™¶QÝJ…QŒÿk€oÚæ»ðhŒsôQ]-g8€‡ÿyò íLÄSº²>ªË`N=ºå&ÚË!ʲHíÕ‹85±LûFØvteÀO6ÕÕk
®Øä%%û3R]½ÀCW~UQ{աѶV*œŒêê%]©°UI«+êê92à¸TW/Rë*$ßS{Õáé·#Øë,¡ºz‰ZWEª:]}Pg «+³ª,ª«-¨u…]…Ú«]i°›ÕÕKñCWöó*Q]må¡+ƒÚ«])d¯Xª«×˜ÔÕÑu ôÇuyft¨®¶BíÕ¹R›É¦°Cú-u•Ø ÿ³Úß^¹7I[×öJŽËŠ[ê*²5,Ò^û¡+s'{ tsW늒dI-eU¸-®²4°4¶>CÑÿÂtæƒå¼½JòÍ/(¢í{Óg¯×É•?ŽÆÜ¢N¦ÌcûY¬á|§V±SÏÀÍÙ«Ò@üÖ×#ŸF¶ñÁy/*Yú¯ö-Ön©«ÌÓÛºVþ’¦ {âê©]å»b7¾Z¿ÂÆG¿¬+_ÖM$¼öœwqye€,^{ÏôÜ{˜)Öˆ¾û^î»®»a]Ÿó’RX1dÝ@»Ðöñ• ã1š_öß²øµ-܇Ôø†»²#±ùлö»Bó$ND£·-ÚÌô*$?Ï0¶Ó qK‰¾)H>âm·ØRí¢#Éôó3£ùšw7 °Ñ)áŸ*FÈÍ¡R·EXb^>’B@§ R{L`Š³yÖ°#!’ZšR»¶.ךâ;zqxø:ÂÈçz sPh»~:Ü0,»Ì¶Å*õþøœ’±?Â^+üÎdyd+µ¦8ÉÒ†ÄÎJîÔ²ö»2)«2Еnl˜¦dtÏv%|ù+ð[ˆ™w’HæÐï˸¾Ý®Ô¡yuý?¤ðôf’ÏéîÙìTàfçLÅÓ±O™ƒ[ O²8!¥GðöpÕðä¸[Îj u½c?¥lªJϳj56Ûœ¦œÐL=™$ðAzO¯&Ù¬+ˆQ†¸Ðª¡hWT¡f!»©° 4MUÃú·pzÃøG€°WØKpþU6Oš¿K¤¶P:z0ÿqYàJOÙ¥[ñ»s(‘Ùæã!±°ÃUolí»Ã»žºð+{åkŠ… «e&.TÈØ»ƒmC4¹Ähñ©íT‹’ø+/à»Ôïܪ›íU€EÊ96m楇NRE-º#¯8JŽ¦~9
™ô+{U˜Pöž#!4ñdÙG&v¸#íCjŠMÂOsâÓª†`v†‡ÿ°]mö¯|25’£‡ýŒþx¢,Ëš¡ºÚ pŠÓfhä_Í=ðx`˜]¤©?àŒÃÂñI`©µG%èî5,UM9ÁR+t‡¢dkÎÇ&sHž*®¶» îø8&6ÖÕÏì>r¼Ãzvê1 )³ ñÒQ÷¯b¨ZfãB©jzÚ-ÍöªvÛU,)}a¶‰É´L!ë±ÇîË(΀uõ+{% ²»©>òÃt•;m~F½dR@âô,ÈóuÊJ~[r&]!|aÄ…pW …ÌÇâúºÊ-üXÖ ·¼ÿǸB[»qŒ®2£M#_RS€3i(D$ýô±¼®/»n;6B’c,ן»¬ZV‰¬NȵèS±DZ?ùˆ3¸ÑØVN¿×Uéˆmi¦dìI‰:ñ¤.XoŒÙÔ•mº²ê[=éÜôs×ÛTÐW`í•ÅO*1¶²Â#ÿc]Åz÷Ô½ÿúåû~nººüADw£½Rˆoa÷Êz¹ºï¨H2-ú‡ºJáyãQP$yðtU¦¾A,ÕÿˆºsH¡Ùîó_ñ¶uMÂ%³Déäq3hú´CîOtUFjùäÚÖ ð6Vw§Ì&]’-XÚ ôìgØíûº*Û»bFùr ñoÉ¥m!ÖÕ¿YEü•§1xg’òœ¯|[WV›J¿ MvraôÓ’-blË×’ÛòÎÜ!u_㛺 C%úí@ûM½ÞXAxXÙT«{ìmÕèØoßò¨#êY¾È×tªu˜J¶¢ª»Ðj™ f˜»½]Ë¡7C&eÃü¾¢«2°j»Ä[!rc‹ˆŒ»M7ž¼ÇsßK¯æ¸f¶5’ʳ¦!æVÞ§;5þ€2õê=^·»D¶*tEîEÏV½ŠµÍÁÚeÆ‹/»sº»›ªO±3 fB=%êèÈ‹ÙÖ飼;,IïâÍ¥åߢhD¥÷mz4÷@Ó-X}×Z-]l;à-ºš»ó.‹·ãêþ¦µ6òÊÃ9]ÉZ’C›.,ö줫Æ3Gr8ñGR³ÝÒu#b%’åÍðw¹Ž¹)E³EW*oå^a[¾¹ãÎ=ºÄÀBÔ-³¹îÚ¯:£ìE´iôÚ «òfQ¨ÆúXW©KLo»³µÄµ®BIƒ¢žœ-Ž(Êxví†)úx ŒÂOç-lê+´AWñöYÁýÐF±¦ê_dgÁŽ-°ö©Jyü1 Õ¬£Ÿ©’x3ë:î¥NÔùÑáüvËÖ9tåd ç~|è·{¤N³-W=»Ä^)f÷ÿb¨û4ç¡yåµfÛæ-ÜÓº®Ju×YùH?ãºá‹µtÙÏ’º aÆ8¨±äGŒ½t®¶$‡Œ_ë’†u]¥w‹^Ǹԕk ¯vÕ-³ÐÉïøí$·ß1KnkCÅ’t’°Ä-ÐȺ®Â»EÞÖUJº0óNUBô†ïgRMÒ¦^˜@Ýø^q¤/À üî-±Ì†½Ÿ×ueßνzOW> +h3Ýcs×’Œo©íá›Q/µúº•Ö’¨|²* p Áh.»:ÁãÃó憆«ºÊ%ª+Lî7;ÝÞ9òCQTMÓŸvˆG†×Í×.? ªg¡?±»n²~†ü¶átVu.ã¾Î«º*»¢ªþ ¹‡ÇTJ¤ËPûøØsTOññ¬Ç}¯ÈŠ¼C=O #ÏY¢ÓÌz̪®œ«UžmàE]ÄYN^|±½..>õ鉺µ®RýíIO¬0xBa u® ¢’¸5‰¯êJ¹ß0øš®b/º`æɸåí¨B¥ï «òGÎ’Ä ÀSžES…ÒÞ»îzÑèš®Rþjù« l×UIJ@Õžd ¯‰W®ýElÿüÔD{ϧŠÃªÓãI©F ÿ’pNØÕdùš®lôÈ:h¯W ¥ÖüÌ[u») 9œæ.¸œO]Íø=olTD-@Â:¥ÍÛÁYUCðìì±¾ìyMWòsNùzú90þŒ.¶é*!I@mâf áJ(ûûdPwâ)Ï3ÌŸž¶¹š2^Ó÷Hy»[·±x .ç_ÝüälÑUA¼uyÒÐñG_nZÉ´õ€B¶+=Ú8ý´©çÜÅ_ÍÁ¬èÊ{vh{}œûîEuA?3ð+ø¤fËA_’w`.âït}èýŸ ñÍÑ%üÚºÓ]IÏ™ûú˜hü»ý3Wu’µ4áÜŸU¬+}7]ÕNæü/ÌgéÕ$ÌŠ®8$4i! îe‰Â…™û³¢«F@v¡(2¨kÚ?>ŽLUêWãÏ/*àiKÃ5§hYWݸ¿ye;? •°:c·¬e]’vˇÝûPW®YdPoqB»¾BÆ,•[ÖU¯a76¡á€¸Bw4³î¼JW’‹,»9Kò¡Ã’®ø´í•ÙN’ãKóvz+ƒû>©×ןðêlÂ1×˺RÓbDK&)* ÉœÑ^¡b’ÂÏ(œp›q^W©9; ì>ß̈õY qzN[ɈO¢Z#IÚOszjYW£Ý£IM²öˆ=ÄèؾM»-bøЪŠ(ðƒ3Fgu’±Z_/ª»oö ºddC â@ÑõÖdæO·hm1ÍbßÚ¨»óÉÂ$øü³ð¿}rtï^aº»éi˜ÑY¸Ì‡ëÏÏÐ˱¼§®Œ¿˜™jIŸÉ-JBüòH·ð×NX5¬Ëe?Õæ?íU÷BK’/™ÖùÌ¿61sU¸¿cN¾òš¹NÍT°ç¢,ÝxØÕhUçá$Õ®íX´6Y8š)]ÁÎß2³‰Îî-8I3″-{©ý-‘Î0X·§ ̺¼Éiª& È:Oè°7Lè v£úš±RêÑïK¯þC»Î°$/úê’ûå>{þu5þM /w`BårˆOlïǺ’Ž òþU)‰IJÞ-F´Æ}°.ˆ‹ØǪó»É…§é¶ëMÀR âòÀŠß- 0æÂcŽf¤+H¥X{‡’röl†½‹èªaª…ýTK¹X ®Ì‹ÄïxÿbBø:Q¸ÒDñĉÓ-¡®6ÂuŒ×ˆ…*»£[ÀP©9,·<_i></_i>
Fd½½!w©å‰¨‰Ù{œõ㪠tgÇÖNµÝm-µøvóЃ¯ÅžÊ^¾Ø¨6£ûûÇ!È™âÁ· ¾Ôf•|Å>÷Þm÷³¾¨Ï:^׺=¯ðíÈK±öîIaçÆUP_™€U…Ü}Ä_Dìб)ùã=f»,ƒ®ØšQ[[îS½¥4ÊÆ!*%SŒ¥‡çúqÐVe^Y¬°ð‹²%áèŽ-‡ôÙcóµ»QŽk4r/5’PÃì©ðˆþ¨ªbʪ³õrEAk=†¢ï†ýÍIªÌñ+ã²› ‡x#™Âì ñæGŒú2h7ØßØè㣯²úM›pyÓ›otr8©¹«VUÃ-FqKü²·Ög¼…ûÿ¶þ>47^s³°¯ì «šùÅQQ^}Õ6T=ÒÊ’uEÕÚd¸¡µ-.˜?!_Ãa@•ãÑ6‰’úîÚëõåûÍÍ-Li-Û7F÷²ž`»fT½&.×лtÕ£ÄB‹Ò¡ÅIÐÐ «l§ ¿ÇD׶ù8kh¥*{0»Ä)½¯8′)£àE=-R0·0‡çe7At_,%èÂåõR™`‹¸l^~IN0ç€ÕPî-€(£çzåSºç¾ Ä©7Úõλñr³BÕinÎêø»»ÙÃ^¬f|ý®~KΡ󰚥Àä*1°žÇêVƒIV_^»¢¾ó~»jFGëk5clöâàå]»‘ÖAŠU$pš‡%X¸¨&¶aÒc?ˆMØã/vé#Ç p±»óðÜ»ÿíþ,-Å¢è+²Ê˜PòÖvV_¸ÌEWæÙïæd¯Ôáåù…E¦~Ó!á†DøìÆ_e‰cÀY}÷z#í©B’¢9)ñž½™uÄì4-MŠdãm§âC‰¼2Ê&hr›×»‹£ãbx… c›-hÌ’q@…öõs,ÃhAÞo/(!r×@J%!Oú_¥}Ãyª’¢ëâ¦òFéKGêa Hã€ÆLσñªÒáÜD-1/}: ?¾C³|ÕêºþàÓú½¯kOüI?(«1oe»» eåo!Vy»Ó`PY®Ÿi»U A’¼ÄfÓÒ}@Á?Xâ_ïŒe©2j(;]ò%íå Ü(ý|TP»AÖ[§…Xùú›7£»²-°ëb6x÷ÿx¤o:Û;jœvL&ª¯ «Z¦®¹}=M’Ö¦ÖCOÚ€,²½¼*¯ÿL^-êrqþµOÍB-P³¶ÞT®&ãÉX/#íFåè6î5‰ÂÖ®j]¬n±=’q‹_î+²9Èèu¡Ï ͵»B¬hôäÔ¦º-Œ{Úö 2ûøš!®Â³÷^©UišÕhM¥¦Žÿ·éLð ¶gVÛ]:µ•ÕÔù³²~ÌQ!¢E j×bÂŽDP»J>â.ô’À27|œõž©» Ö€ow‰;´vC¦í»o¤zÈ1»??’ ÆÂI+U’ @ -WÄ g%’çF$¡Þµøv8°²÷¶ÞQÓÕßɦÓÿª²(£ 4[(Eï(ø.K¨q›²(R;KÅgô[aat{¡’°âŒ @öQ£9rhäˆã’ƒfŸ¾Ÿ;æ»î×jÐ%ছúº»-é~&£»‘Då01ûl±’rÌî¼kÃ;Òx2ÐùêI»RSïÛ9ý0gìè)ym§ß’f.èEfôrCQ›ªž8K;Æ:Ûb‡(‘¦… äÏmÌÜBÄa`½+[Î_0Ÿµe-Á;r`m¡ð¡r°¾‹ª0¯#‰îgô×5‰ð)[Âx’ì P´¹‡>R#ì^Ø£ã«Tz¡>LŒExîÎL I{×q‰m’g Ãî°ûZ²-´Gäy®ë>-£10_CŒZrE-ö VP†èàØŠ £åhEá˜QÑKƒ’7Ø+·¡hǵ}ر ëòÑ·%ü^üŒXì•À¢!67:Úù» 1ù šzX£²`rˆ¹v«Z@Úöt»É’àÒç¨XfGAA¡Öz¶•’Ù$^¼aðÎQÞ’œ:¤.Õq‰fº¨ˆþ{8?»Í[æÎ-Ïéuä*-öˆÊ ˆ×^ŸC¡»£]äjW!½»î^ F-¶Üü 0[M:Ð’#’ÅäîúhXr Xò vöÖ|Ñ.·/…^¼i/À@¼¯žÈd1Ι‰êõ¶ævk»¥ŸtDi¤iQÅD»ªÂ:¸Ì¶ƒó9Ö =™»4ç5ëP rUqÕSs!íLSø¶‹ÊƒE BÒÎ39‹µªðòÆëò{(¤s©z`»ÀÅɬ#‹¦Ñ2:OÙHóö3CÙ»o%ÈXÊíP«ÇX‰Ì’÷A6Žê*‡¨õˆu÷wTä»ËpÔ]†=NÂÇ ³§7í¥EóÕWéZZ(…ökM vmcGr4j$TQ~ÆA†ñhÃ¥†+ÍÓå¡~³[ÇE0(«aèƒ!¬Í궾’êƒ#W #OýŠ@•†:ÆÕh 1RDëm@Aö »çæn ÖÊÆ9îæÍ1 ðéÞè!e!.’Ó^þö¹±:¸Ô;í°M»ŸZDU ‰Lk~¹§»§Ç¹§gš]ãtθ2½0û5m°-¡ŒÙ$˜õ;WŽ.õŽ•¶¥ç·z • ‹+ëƒUØ©GÊߦÄÿêË’-Ÿ;µ¯Àd?l»É€ãRùþ-6þÒ;’Ößö2Ê¿cŽ+Û2 Ì]XRTsïÌÛn€+;åD XX§;Çœ˜ñŸaž¥ çT¬Î‰š£FîÉ#)õ»‘†ICÃàÅî}Åúþ™· †äñË™Šˆð=¸Maú£UášúŒAÉ(ª»½ý¬¶_k
â‰5Oo@Cã¶RGU»jšÏ-Ž _+ÑÙ³->m¦¨¦øÏF@žÆ`t ì|Õö¹M}³gȹ|…HM‰ZUaÃ’+©Vèk*«š‡lHÓÐ/+V:wª9″_ðלtÚû-QeÁ£C¿?ö+U®Bd•eÎß¹øû.+¯Xïg0}ÛãJ³È_Ùj;R Ì0uUdúW‰@À’Xõæ~1ûìM¡ãVUlÃíÀ¥‡aèÍpŒ»Ï’ü¯ÎVhÕºµn¯¬Ü){ðõ´4¦¶$ÉxÆÏrPÕu8sÝ»}T± Vw¸M´Ñ›Êˆæ¥¯Ü’õ†éžç¹~ÆóÔ³f»Á&cÓfWáT»ŠÀùŸú²ä¥Å;àn(l³‰8̇»‘Û{ñ*ÿÍ=ž‡ÁæðCu>bj]cc-€ô-«Ûrµ$’´,bÄ·§ym£,«£»«7¿®’Û3v_Iئ2S3H8ŒÍ»ßèY¢ÑW©(ĥ͒QÁ€nÁßvYmW†ÞK»ñÄ¿Å®À•}¾ÈÃk…²ÆÎÏèÂ^ºQo:°-=u>•cu²F¹¥{ûO þ]‰¶*·² |7;½«»/r†¬úH/™}5Û`}éy®ÎÉUHE|Ö¸¹Hôæmv«*>O.kìÒâi:²¸û|˜Ølò@úTפHqÐë’kùŸL·;½O-6Ò ª³°zǧxòhy蛵Å5:æLØH±*=t ö©›¶±»Æ0*5·hOꫬ0″Ö?VÆzõãh#8U²C+-½©)îH@#f™V ,XZ;ZœŠÕX! n@Ñ1ìZBSSæLé«’‡°Pq¬ªocΈ-(ÛÇ™Y8º¢ÀÂÀúÅÇUÊÿÄý:®Û ‘T~êEÃ)}%q%Œ ÖÇe0H’œÚ+††C|FfÌaL{ç’¯|¤åS/Oé«Øå ¤Ëí~«>m{â¥ö·äKj+ˆböøbzÎÒ,*¤,›ھƒ¿ÔÔG_Åc¯øµr?z!uV4′»3ˆûØhWªH†‰³¹Ûiù$¦ *XÛöåc«¬ †{ãÀψ›?ôU2¼•T]É£^¡ÛãAäÒƒ’$_Dunã;´|¡€nÓß ÈvëÜ扚v UÃi{}wÁêÌýiÉUW*}¿]ýIñ‰ziq¯öë%Sƒ2øêî[±Bp»eðòΚB»5B›Ð±‰BÙEø¾euçÒó¸ã³1¹JæQ·n†z¹Èi‰¤cSr&®¦+Xi»o/?úÊóR.ÕMÆË¢cÇZ £QÚ¶An:Ž¿ýÍ!aØ=lCnÍCkƒ-0{¢ÚÔxðT£I8Ò’ù»>’.rlfÎßX¼›HØ=ÔwÈW!&]† a»…V Ð 0ж™RJ’#ÅûÒÉFû%GMcG(,’½ÃgJ®Î»6Ãb!](†…kç YÊïUÚâ´B,ì’,»§7uL®ìÉî1NTÎ’yLû&2ÇǨ-W‡öužf‹ v§ f~äX:+Hê[UEI=7mD®ÜÝø?ŒVƒó蜫Ñ]BÇg(‘ÂòVÓéN.s€ºÜDz{œh5¤ó(èÃåÉÌšFH‡ýŸC¹zîg çCˆ¹;ÚÑ5’X|»‘€¾K¦´œ›ü¿]:pjÛ$âw¨ãhÎ 9ÎÂÕ7Êdlíä*á«lE$£ï.èì 1’ÚêÍf°a¦Ä™ç!Ñ׳0Sçì¹›ŒR öå*wåøòÐÍL@oÛž*?«DïÀaŠØj@Rw$Ç íÏZƒ½dJ«ü€žheè[FJ}¹*Ô}{ŸëïêtgÔÒjV¤jAÓ¤gO0!§ò @3Zn `Goï q†¬î®ib+t€n÷Ü9ÍX ëÍ»ïnpã@ëIH%a»‡L›6s:r…d˜ã†‡,O…Î@u5þƒv×b†`ÅÎÉKˆN[vâó¨eQË.UCkžù6ârSeõm¹ÒqSܹQâ¢7oÆßJù;ˆ=»fÿ1iÚD8¦-mú»ÁiÜ Ów¼ðΠХq§U绯µÅ[Û§äØ ÔWÃYJ]»Æß¹ÅÅS)P1v°ì·¥¦øP›¥`-ÓŽb´CNGà§NÐ=pfÄÇŸÕë^>(ÁOI™’W»šˆu{+Xê¨UV’sGM@ çæ‡fŸ†žšñ!Ͻ¥¯y¸B€u€ú[Ìü@A¹-P>ÝipËQ=•et?¶q#:-},å‰é8É¢ÄóûëW®¬c§òkT¢ˆ(†H6v~î&ø69,&N>^ä<_></_>
- Мустафин Р. И., Буховец А. В., Протасова А. А., Шайхрамова Р. Н., Ситенков А. Ю., Семина И. И. Сравнительное исследование поликомплексных систем для гастроретентивной доставки метформина. Разработка и регистрация лекарственных средств. 2015; 1(10): 48–50.
- Wise, «Review of the History of Medicine» (Л., 1967).
- М.П. Киселева, З.С. Шпрах, Л.М. Борисова и др. Доклиническое изучение противоопухолевой активности производного N-гликозида индолокарбазола ЛХС-1208. Сообщение I // Российский биотерапевтический журнал. 2015. № 2. С. 71-77.
- https://reshator.com/sprav/algebra/8-klass/rastyazhenie-i-szhatie-grafikov-funkcij/.
- https://reshator.com/sprav/algebra/10-11-klass/preobrazovaniya-grafikov-trigonometricheskih-funkcij/.
- https://studfile.net/preview/3540104/page:4/.
- https://www.eduportal44.ru/npo/kadk/SiteAssets/111/Forms/AllItems/17.06.2020%20%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0%2011%D0%AD%20%D0%B3%D1%80%D1%83%D0%BF%D0%BF%D0%B0%20(2).pdf.
- Frédault, «Histoire de la médecine» (П., 1970).
- Скориченко, «Доисторическая M.» (СПб., 1996); его же, «Гигиена в доисторические времена» (СПб., 1996).
- Renouard, «Histoire de la medicine» (П., 1948).