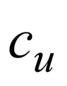Список функций, изученных в 7 и 8 классе
Функция | Формула | График | Раздел справочника |
Прямая пропорциональность | y = kx | Прямая | 7 кл., §37 |
Линейная функция | y = kx+b | Прямая | 7 кл., §38-39 |
Обратная пропорциональность | $ y = frac{k}{x} $ | Гипербола | 8 кл., §6 |
Квадрат числа | $ y=x^2$ | Парабола | 8 кл., §18 |
Квадратный трёхчлен | $ y = ax^2+bc+c$ | Парабола | 8 кл., §28-29 |
Квадратный корень | $ y = sqrt{x}$ | Парабола | 8 кл., §22 |
Растяжение и сжатие графика по оси OX
Сравним графики пар функций, которые в общем виде можно записать так:
$$ y_1 = f(x), y_2 = f(px) $$
где $p gt 1$, произвольный положительный множитель.
Пусть p = 2.
Парабола: $y_1 = f(x) = x^2$ $ y_2 = f(2x) = (2x)^2 = 4x^2 $ $y_2 = y_1 при x_2 = frac{1}{2} x_1$ График сжимается в 2 раза по оси OX |  |
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = f(2x) = frac{4}{(2x)} = frac{2}{x}$ $ y_2 = y_1 при x_2 = frac{1}{2} x_1 $ График сжимается в 2 раза по оси OX |
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = f(2x) = sqrt{2x}$ $y_2=y_1 при x_2 = frac{1}{2} x_1$ График сжимается в 2 раза по оси OX |
|
Теперь сравним пары функций с делением на p:
$$ y_1 = f(x), quad y_2 = f left( frac{x}{p} right), quad p gt 1 $$
Пусть p = 2
Парабола: $y_1 = f(x) = x^2$ $ y_2 = f left(frac{x}{2}right) = left(frac{x}{2}right)^2 = frac{x^2}{4} $ $y_2 = y_1 при x_2 = 2x_1$ График растягивается в 2 раза по оси OX |  |
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = f left(frac{x}{2}right) = frac{4}{x/2} = frac{8}{x}$ $ y_2 = y_1 при x_2 = 2x_1$ График растягивается в 2 раза по оси OX |
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = f left(frac{x}{2}right) = sqrt{frac{x}{2}}$ $y_2=y_1 при x_2 = 2x_1$ График растягивается в 2 раза по оси OX |
|
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = f(px), quad p gt 1 $$
график второй функции сжимается в p раз по оси OX по сравнению с графиком первой функции.
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = f Biggl(frac{x}{p}Biggr), quad p gt 1 $$
график второй функции растягивается в p раз по оси OX по сравнению с графиком первой функции.
Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)
Растяжение и сжатие графика по оси OY
Сравним графики пар функций, которые в общем виде можно записать так:
$$ y_1 = f(x), quad y_2 = Af(x) $$
где $A gt 1$, произвольный положительный множитель.
Пусть A = 2.
Парабола: $y_1 = f(x) = x^2$ $ y_2 = 2f(x) = 2x^2 $ $y_2 = 2y_1 при x_2 = x_1$ График растягивается в 2 раза по оси OY |  |
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = 2f(x) = frac{8}{x}$ $ y_2 = 2y_1 при x_2 = x_1$ График растягивается в 2 раза по оси OY |
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = 2f(x) = 2sqrt{x}$ $y_2 = 2y_1 при x_2 = x_1$ График растягивается в 2 раза по оси OY |
|
Теперь сравним пары функций с делением на A:
$$ y_1 = f(x), quad y_2 = frac{1}{A} f(x), quad A gt 1 $$
Пусть A = 2
Парабола: $y_1 = f(x) = x^2$ $ y_2 = frac{1}{2}f(x) = frac{x^2}{2}$ $y_2 = frac{1}{2}y_1 при x_2 = x_1$ График сжимается в 2 раза по оси OY |  |
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = frac{1}{2}f(x) = frac{2}{x}$ $ y_2 = frac{1}{2}y_1 при x_2 = x_1$ График сжимается в 2 раза по оси OY |
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = frac{1}{2}f(x) = frac{sqrt{x}}{2}$ $y_2 = frac{1}{2}y_1 при x_2 = x_1$ График сжимается в 2 раза по оси OY |
|
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = Af(x), quad A gt 1 $$
график второй функции растягивается в A раз по оси OY по сравнению с графиком первой функции.
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = frac{1}{A} f(x), quad A gt 1 $$
график второй функции сжимается в A раз по оси OY по сравнению с графиком первой функции.
Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)
Примеры
Пример 1. Постройте в одной координатной плоскости графики функций:
$$ y = sqrt{x}, y = sqrt{3x}, y = sqrt{frac{x}{3}}, y = 3sqrt{x} $$
Сделайте выводы.

По сравнению с графиком $y = sqrt{x}$:
- график функции $y = sqrt{3x}$ сжимается в 3 раза по оси OX(←)
- график функции $y = sqrt{frac{x}{3}}$ растягивается в 3 раза по оси OX(→)
- график функции $y = 3sqrt{x}$ растягивается в 3 раза по оси OY(↑)
Пример 2*. Постройте в одной координатной плоскости графики функций:
$$ y = f(x), y = f(2x), y = f Biggl(frac{x}{2}Biggr), y = 2f(x) $$
где $f(x) = x^2+3x+2$
Сделайте выводы.
Исходная функция $y = f(x) = x^2+3x+2$
Остальные функции
$$ y = f(2x) = (2x)^2+3 cdot (2x)+2 = 4x^2+6x+2 $$
$$ y = fBiggl(frac{x}{2}Biggr) = Biggl(frac{x}{2}Biggr)^2+3 cdot Biggl(frac{x}{2}Biggr) +2 = frac{x^2}{4}+ frac{3}{2} x+2 $$
$$ y = 2f(x) = 2x^2+6x+4 $$
Получаем:

По сравнению с графиком $y = f(x) = x^2+3x+2$:
- график функции y = f(2x) сжимается в 2 раза по оси OX(→)
- график функции $y = f left(frac{x}{2}right)$ растягивается в 2 раза по оси OX(←)
- график функции y = 2f(x) растягивается в 2 раза по оси OY(↑)
Рейтинг пользователей
?
: , *-* + : ? ! ? ! >>> mathprofi.com
15% () 5530-hihi5 : >>> , , | , . , . , . , , , . . ? — , , . , , ? , , . /, , . , , ! ? , , . ! , . , , ! , , , , , .. , , , . , , , . , : , . , , . , . , . , . . . : , . , , : . , , . , (); ; ; (); ; ; ; ; . : () () .. : , . : , , . , : 1 . , :
, , .., , . , . . 2 :
, . , : 2-3 : , , . — ! , . 2 3 :
. : ( ). , , . , . : , , . : 3 :
2 :
, . 2 : , . / , , : 4 . :
. : () (). , . : , ? , , : . : , . ( ). : 5 :
, . , . : . 2 : . : . . . , / . , , . /, ( ) . : : 1) , ; 2) , . 6 1 :
, . , , ( ) 2 . : 7 ( ) 2 :
, . , ( ) ( ). , ( ). : 8 ( ) :
. ! , , , , , . ( ). . , : , , . ? , , , , // , . , : : 1) ( ) ( ) 2) ( ) (!!!) , . 9 : ( ): 1) 2) (!!!) : ( ):
, . , . : 10 . : . : 1) 2 : ; 2) : ; 3) (!!!) : :
, , . , /. . , , . () .. 1) , . : , , . 2) , . : , , . , =) 11 . /:
2 :
, (, ) , 2, : . 2 :
, , : . , — , , ( 1,3) . . ! , , / : 12 . : . 2 :
, 2 , ( ). : . , . : , . : , . 13 :
: 14 :
, . . , . , , : ( ) , . . /. Ƞ , ( ) . : : 1) , ; 2) , . 15 . , , :
: 1) () . , . 2) . 16 ( ): 1) 1,5 : ( ); 2) 2 : :
, : 17 : 1) : ; 2) 4 : :
, , , , , . : 18 : 1) 2 : ; 2) : ; 3) 1 : :
, 1 . (. 7). : , . : , (. ), ; , , . : 19 ( 10) 10 , . . : 4) : ; 5) 3 : :
, , , : 5 3 . , . 5 , 1 . .. , ! , . , — , , , , , : 20 , . . . , , , . , , . . : , . : , . , : : : , : . : 1) : ( ); 2) 2 : ( ); 3) : ( ):
: 21 . . : (1) 1 . , . (2) . . . (3) . , . (4) . . ( ): 1) 1 : ( ); 2) : ( ); 3) : ( ):
, . pdf-, , . , . , . . . , , , , . , , . : : , . 22 :
, :
:
, , . . , , . ? : , . : . : , , (. 13). 23 , :
: , , . : .. (, ). , , . : : , , , . , 24- , =) 24 , :
, , , , :
: ! ! : , , , . , , , , : , : . : 25 :
, , , :
, : . , : , , . , . ? . : . : . , , . : 26 . =)
, , :
, ? , . : , : , . , , . =) — , , . , =) ! : >>> ( ) ? ! — |
Преобразование графиков функций
Анна Малкова
В этой статье мы расскажем об основных преобразованиях графиков функций. Что нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали. Как задать растяжение графика по горизонтали или вертикали. Как отразить график относительно оси Х или Y.
Очень жаль, что эта тема — полезная и очень интересная — выпадает из школьной программы. На нее не постоянно хватает времени. Из-за этого многим старшеклассникам не даются задачи с параметрами — которые на самом деле похожи на конструктор, где вы собираете решение из знакомых элементов. Хотя бы для того, чтобы решать задачи с параметрами, стоит научиться строить графики функций.
Но конечно, не только для того, чтобы сдать ЕГЭ. Первая лекция на первом курсе технического или экономического вуза посвящена функциям и графикам. Первые зачеты в курсе матанализа связаны с функциями и графиками.
Начнем со сдвигов графиков по Х и по Y.
Сдвиг по горизонтали.
Пусть функция задана формулой и Тогда график функции сдвинут относительно исходной на а вправо. График функции сдвинут относительно исходной на а влево.

1. Сдвиг по вертикали.
Пусть функция задана формулой и С — некоторое положительное число. Тогда график функции сдвинут относительно исходного на С вверх. График функции сдвинут относительно исходного на С вниз.

Теперь растяжение графика. Или сжатие.
2. Растяжение (сжатие) по горизонтали.
Пусть функция задана формулой и Тогда график функции растянут относительно исходного в k раз по горизонтали, если , и сжат относительно исходного в k раз по горизонтали, если

3. Растяжение (сжатие) по вертикали
Пусть функция задана формулой и Тогда график функции растянут относительно исходного в М раз по вертикали, если , и сжат относительно исходного в М раз по вертикали, если

И отражение по горизонтали.
4. Отражение по горизонтали
График функции симметричен графику функции относительно оси Y.


5. Отражение по вертикали.
График функции симметричен графику функции относительно оси Х.

Друзья, не возникло ли у вас ощущения, что вы все это где-то видели? Да, наверняка видели, если когда-либо редактировали изображения в графическом редакторе на компьютере. Изображение можно сдвинуть (по горизонтали или вертикали). Растянуть (по горизонтали или вертикали). Отразить. И все это мы делаем с графиками функций.
И еще два интересных преобразования. Здесь в формулах присутствует знак модуля. Если не помните, что такое модуль, — срочно повторите эту тему.
6. Графики функций и
На рисунке изображен график функции Она специально взята такая — несимметричная относительно нуля.

Построим график функции
Конечно же, мы пользуемся определением модуля.
Это мы и видим на графике. Для неотрицательных значений х график остался таким же, как был. А вместо каждого отрицательного х мы взяли противоположное ему положительное число. И поэтому вся та часть графика функции, что лежала слева от оси Х, заменилась на зеркально отраженную правую часть графика.

Теперь график функции Вы уже догадались, что будет. Вся часть графика, лежащая ниже оси Х, зеркально отражается в верхнюю полуплоскость. А верхняя часть графика, лежащая выше оси Х, остается на месте.

Как определить по формуле функции, будет график преобразован по горизонтали (по Х) или по вертикали (по Y)? Разница очевидна. Если сначала мы что-либо делаем с аргументом х (прибавляем к нему какое-либо число, умножаем на какое-либо число или берем модуль) — преобразование по Х. Если сначала мы нашли функцию, а затем уже к значению функции что-то прибавили, или на какое-нибудь число умножили, или взяли модуль, — преобразование по Y.
Вот самые простые задачи на преобразование графиков.
1. Построим график функции
Это квадратичная парабола, сдвинутая на 3 влево по x и на 1 вниз по y.
Вершина в точке

2. Построим график функции
Выделим полный квадрат в формуле.
График — квадратичная парабола, сдвинутая на 2 вправо по x и на 5 вниз по y.
Обратите внимание: график функции пересекает ось y в точке На нашем графике это точка

Продолжение — в статье «Построение графиков функций».
Преобразования графиков тригонометрических функций
Общие принципы преобразования графиков функций изучались нами в главе 8, (см. §47, §48, §50 справочника для 8 класса). В этом параграфе мы рассмотрим особенности тригонометрических функций при использовании этих преобразований.
п.1. Растяжение и сжатие графиков тригонометрических функций по оси OX
Общие принципы растяжения и сжатия графиков по оси OX:
При сравнении графиков двух функций $$ y_1=f(x), y_2=f(px), pgt 1 $$ график второй функции сжимается в p раз по оси OX по сравнению с графиком первой функции.
При сравнении графиков двух функций $$ y_1=f(x), y_2=f(frac{x}{p}), pgt 1 $$ график второй функции растягивается в p раз по оси OX по сравнению с графиком первой функции.
Эти принципы справедливы и для тригонометрических функций.
Тригонометрические функции являются периодическими: синус и косинус с периодом 2π, тангенс и котангенс — с периодом π. Получаем следствие общих принципов:
При сравнении двух тригонометрических функций $$ y_1=f(x), y_2=f(px), pgt 1 $$ период второй функции уменьшается в p раз: $$ T_2=frac{T_1}{p} $$
При сравнении двух тригонометрических функций $$ y_1=f(x), y_2=f(frac{x}{p}), pgt 1 $$ период второй функции увеличивается в p раз: $$ T_2=pT_1 $$
Например:
Построим в одной системе координат три графика: $$ f(x)=sinx, g(x)=sin2x, h(x)=sinfrac{x}{2} $$ 
Период колебаний функции (g(x)=sin2x) в 2 раза меньше: (T_g=frac{2pi}{2}=pi).
Период колебаний функции (h(x)=sinfrac{x}{2}) в 2 раза больше: (T_h=2cdot 2pi=4pi).
п.2. Растяжение и сжатие графиков тригонометрических функций по оси OY
Общие принципы растяжения и сжатия графиков по оси OY:
При сравнении графиков двух функций $$ y_1=f(x), y_2=Af(x), Agt 1 $$ график второй функции растягивается в A раз по оси OY по сравнению с графиком первой функции.
Общий принцип сжатия графиков:
При сравнении графиков двух функций $$ y_1=f(x), y_2=frac{1}{A}f(x), Agt 1 $$ график второй функции сжимается в A раз по оси OY по сравнению с графиком первой функции.
Эти принципы справедливы и для тригонометрических функций.
Т.к. для графиков синуса и косинуса (синусоиды) характерна амплитуда колебаний, то также говорят, что:
- умножение на параметр (Agt 1) увеличивает амплитуду колебаний в (A) раз;
- деление на параметр (Agt 1) уменьшает амплитуду колебаний в (A) раз.
Например:
1) Построим в одной системе координат три графика: $$ f(x)=cosx, g(x)=2cosx, h(x)=frac{1}{2}cosx $$ 
Умножение на (A=2) увеличивает амплитуду колебаний в 2 раза.
Область значений функции (g(x)=2cosx: yin[-2;2]). График растягивается по оси OY.
Деление на (A=2) уменьшает амплитуду колебаний в 2 раза. Область значений функции (h(x)=frac12 cosx: yinleft[-frac12; frac12right]). График сжимается по оси OY.
2) Теперь построим $$ f(x)=tgx, g(x)=2tgx, h(x)=frac{1}{2}tgx $$ 
В этом случае хорошей иллюстрацией растяжения по оси OY при умножении и сжатия по оси OY при делении на (A=2) служит поведение функции при (x=fracpi4). $$ fleft(fracpi4right)=tgleft(fracpi4right)=1, gleft(fracpi4right)=2tgleft(fracpi4right)=2, hleft(fracpi4right)=frac12 tgleft(fracpi4right)=frac12 $$ Аналогично — для любого другого значения аргумента x.
п.3. Параллельный перенос графиков тригонометрических функций по оси OX
Общие принципы переноса по оси OX:
При сравнении графиков двух функций $$ y_1=f(x), y_2=f(x+a), agt 0 $$ график второй функции смещается влево на a по оси OX по сравнению с графиком первой функции.
При сравнении графиков двух функций $$ y_1=f(x), y_2=f(x-a), agt 0 $$ график второй функции смещается вправо на a по оси OX по сравнению с графиком первой функции.
Эти принципы справедливы и для тригонометрических функций.
При этом параметр x называют начальной фазой колебаний.
При сравнении двух тригонометрических функций (y_1=f(x)) и (y_2=f(xpm a)) говорят, что у второй функции сдвиг по фазе равен (pm a).
Например:
1) Построим в одной системе координат три графика: $$ f(x)=sinx, g(x)=sinleft(x+fracpi4right), h(x)=sinleft(x-fracpi4right) $$ 
Функция (g(x)=sinleft(x+fracpi4right)) сдвинута на (fracpi4) влево по сравнению с (f(x))
Функция (h(x)=sinleft(x-fracpi4right)) сдвинута на (fracpi4) вправо по сравнению с (f(x))
п.4. Параллельный перенос графиков тригонометрических функций по оси OY
Общие принципы переноса по оси OY:
При сравнении графиков двух функций $$ y_1=f(x), y_2=f(x)+a, agt 0 $$ график второй функции смещается вверх на a по оси OY по сравнению с графиком первой функции.
При сравнении графиков двух функций $$ y_1=f(x), y_2=f(x)-a, agt 0 $$ график второй функции смещается вниз на a по оси OY по сравнению с графиком первой функции.
Эти принципы справедливы и для тригонометрических функций.
Например:
1) Построим в одной системе координат три графика: $$ f(x)=sinx, g(x)=sinx+1, h(x)=sinx-1 $$ 
Функция (g(x)=sinx+1) сдвинута на 1 вверх по сравнению c (f(x))
Функция (h(x)=sinx-1) сдвинута на 1 вниз по сравнению с (f(x))
п.5. Общее уравнение синусоиды
Синусоида — плоская кривая, которая задается в прямоугольной системе координат уравнением: $$ y(x)=Asin(cx+d)+B $$ где
A — амплитуда, характеризует растяжение графика по оси OY
B — вертикальный сдвиг, характеризует сдвиг графика по оси OY (вверх/вниз)
c — циклическая частота, характеризует период колебаний и растяжение графика по оси OX
d- начальная фаза, характеризует сдвиг графика по оси OX(влево/вправо)
График (y(x)=Acos(cx+d)+B) также называют синусоидой. Термин «косинусоида» употребляется относительно редко.
Поскольку график косинуса получается из графика синуса сдвигом по фазе на π/2 влево, вводить термин «косинусоида» излишне.
Например:
Построим график (g(x)=3sinleft(2x+fracpi2right)-1)
По сравнению с (f(x)=sinx):
- (A=3) — график растянут по оси OY в 3 раза
- (c=2) — период меньше в 2 раза T=π, график сжат в 2 раза по оси OX
- (d=fracpi2) — начальная фаза положительная, график сдвинут на (frac{pi}{2cdot 2}=fracpi4) влево
- (B=-1) — график сдвинут по оси OY на 1 вниз

п.6. Общее уравнение тангенцоиды
Tангенцоидa — плоская кривая, которая задается в прямоугольной системе координат уравнением: $$ y(x)=Atg(cx+d)+B $$ где
A — амплитуда, характеризует растяжение графика по оси OY
B — вертикальный сдвиг, характеризует сдвиг графика по оси OY (вверх/вниз)
c — циклическая частота, характеризует период колебаний и растяжение графика по оси OX
d- начальная фаза, характеризует сдвиг графика по оси OX(влево/вправо)
График (y(x)=Actg(cx+d)+B) также называют тангенцоидой.
Например:
Построим график (g(x)=frac12 tgleft(frac{x}{2}-fracpi3right)+1)
По сравнению с (f(x)=tgx):
- (A=frac12) — график сжат по оси OY в 2 раза
- (c=frac12) — период больше в 2 раза T=2π, расстояние между асимптотами 2π, график растянут в 2 раза по оси OX
- (d=-fracpi3) — начальная фаза отрицательная, график сдвинут на (frac{pi}{3cdot 1/2}=frac{2pi}{4}) вправо
- (B=1) — график сдвинут по оси OY на 1 вверх

п.7. Примеры
Пример 1.Постройте в одной системе координат графики: $$ f(x)=sinx, g(x)=-sinx, h(x)=cosx $$ Найдите сдвиг по фазе для (g(x)) и (h(x)) в сравнении с (f(x)).

Сдвиг по фазе удобно определять по главной арке синусоиды.
Для (f(x)=sinx) главная арка определена на отрезке (0leq xleq pi)
Для (g(x)=-sinx) главная арка определена на отрезке (-pileq xleq 0), т.е. сдвинута на π влево от (f(x)). Это означает, что: $$ f(x)=g(x+pi), sinx=-sin(x+pi) $$ Для (h(x)=cosx) главная арка определена на отрезке (-fracpi2leq xleq fracpi2), т.е. сдвинута на (fracpi2) влево от (f(x)). Это означает, что: $$ f(x)=hleft(x+fracpi2right), sinx=cosleft(x+fracpi2right) $$
Пример 2. Найдите наименьшие положительные периоды функций:
a) (y=sin5x)
Период синуса (2pi) уменьшается в 5 раз. Получаем: (T=frac{2pi}{5})
б) (y=cospi x)
Период косинуса (2pi) уменьшается в (pi) раз. Получаем: (T=frac{2pi}{pi}=2)
в) (y=tgfrac{x}{4})
Период тангенса (pi) увеличивается в 4 раза. Получаем: (T=4pi)
г) (y=tgleft(2x+frac{pi}{3}right))
Период тангенса (pi) уменьшается в 2 раза. Получаем: (T=fracpi2)
Пример 3. Используя правила преобразования графиков функций, постройте график $$ f(x)=2ctgleft(3x+fracpi6right) $$ По сравнению с (g(x)=tgx):
- (A=2) — график растянут по оси OY в 2 раза
- (c=3) — период меньше в 3 раза (T=fracpi3), расстояние между асимптотами (fracpi3), график сжат в 3 раза по оси OX
- (d=-fracpi6) — начальная фаза положительная, график сдвинут на (frac{pi}{6cdot 3}=frac{pi}{18}) влево
Расположение нулей: $$ tgleft(3x+fracpi6right)=0Rightarrow 3x+fracpi6=pi kRightarrow 3x=-fracpi6+pi kRightarrow x =-frac{pi}{18}+frac{pi k}{3} $$ Вертикального сдвига нет, нули расположены на оси OX.
Расположение асимптот: $$ 3x+fracpi6nefracpi2+pi kRightarrow 3xnefracpi3+pi kRightarrow xnefracpi9+frac{pi k}{3} $$ Пересечение главной ветви с осью OY: (x=0, y=2tgfracpi6=frac{2}{sqrt{3}})
С учетом периода (fracpi3) получаем семейство дополнительных точек для построения графика (left(frac{pi k}{3}; frac{2}{sqrt{3}}right)).

Пример 4. Определите графически, сколько корней имеет уравнение на отрезке: a) (sinx=sin2x) при (0leq xleq 3pi)

Ответ: 7 корней
б) (cosfrac{x}{2}=cos2x) при (-2pileq xleq 2pi)

Ответ: 7 корней
- Wise, «Review of the History of Medicine» (Л., 1967).
- Frédault, «Histoire de la médecine» (П., 1970).
- Киржанова Е. А., Хуторянский В. В., Балабушевич Н. Г., Харенко А. В., Демина Н. Б. Методы анализа мукоадгезии: от фундаментальных исследований к практическому применению в разработке лекарственных форм. Разработка и регистрация лекарственных средств. 2014; 3(8): 66–80. DOI: 10.33380/2305-2066-2019-8-4-27-31.
- https://reshator.com/sprav/algebra/8-klass/rastyazhenie-i-szhatie-grafikov-funkcij/.
- https://www.mathprofi.ru/kak_postroit_grafik_funkcii_s_pomoshyu_preobrazovanii.html.
- https://ege-study.ru/preobrazovanie-grafikov-funkcij/.
- https://reshator.com/sprav/algebra/10-11-klass/preobrazovaniya-grafikov-trigonometricheskih-funkcij/.
- Bangun H., Aulia F., Arianto A., Nainggolan M. Preparation of mucoadhesive gastroretentive drug delivery system of alginate beads containing turmeric extract and anti-gastric ulcer activity. Asian Journal of Pharmaceutical and Clinical Research. 2019; 12(1):316–320. DOI: 10.22159/ajpcr.2019.v12i1.29715.
- Guardia, «La Médecine à travers les âges».





















 , ).
, ).